X 2 = b Front Porch Math > > Solving Equations of the Form ax2 =b a x 2 = b Example 1 1 18 = 2x2 18 = 2 x 2 Lets start with the equation y = 2x2 y = 2 x 2 If we want to show all the possible solutions we would need to graphing this equation Then we find out that y = 18 y = 18, so the equation becomes 18 = 2x2 18 = 2 x 2As an example of the claim, (y Ñ1) = 2(x 4) is a line of slope 2 that passes through the point in the plane (4;1) 144 Claim y = ax is a line of slope a that contains the point (0,0) Proof This claim follows from the previous claim if we write y = ax as y = ax 0 The previous claim tells us that y ax 0 a line of slope a that contains theWorking backwards Example Find the equation of the following parabola of the form y = ax 2 The graph is of the form y = ax 2 The given coordinate is ( 2, 1 ) So x = 2 and y = 1 are on the curve Substitute and solve
Mathematics Upper Secondary Ydp Student Activity The Functions Y Ax 2 Q
Y=ax^2+bx+c find a b c
Y=ax^2+bx+c find a b c- Get the equation in the form y = ax2 bx c Calculate b / 2 a This is the x coordinate of the vertex To find the y coordinate of the vertex, simply plug the value ofFind the quadratic function y = ax^2 bx c whose graph passes through the given points (−1,−3), (3,25), (−2,5) Hint Substitute each point into y= ax^2 bx c to get a system of linear equations, then solve check_circle




Graphing Quadratic Functions Y Ax 2 Bx C
Y = ax 2 bx c Move the loose number over to the other side y – c = ax 2 bx Factor out whatever is multiplied on the squared term Make room on the lefthand side, and put a copy of "a" in front of this spaceRewrite the equation as ax2 bx c = y a x 2 b x c = y Move y y to the left side of the equation by subtracting it from both sides Use the quadratic formula to find the solutions Substitute the values a = a a = a, b = b b = b, and c = c−y c = c y into the quadratic formula and solve for x x Simplify the numeratorTry varying the values of a and k and examine what effects this has on the graph
If the graph of $y = f(x) = ax^2 bx c$ passes through $(1,0)$ and $(3,0)$ this means that $f(1) = 0$ and $f(3) = 0$ One such quadratic polynomial is $$ f(x) = (x1)(x3) = x^2 4x 3 $$ Since multiplying the polynomial $f(x)$ by a real number $k$ will not influence the value of $f(x)$ at $1$ and $3$ we find that the graph of $$ f(x) = k(x1)(x3) = k(x^2 4x 3) $$ also passes throughIsolating "y" and then making a function with the quadratic formula to x deltaThe vertex is on the axis of symmetry, so its $x$coordinate is 3 The vertex is also a point on the parabola, so it satisfies the equation for the parabola This means that if you plug the $x$coordinate of the vertex into the equation, you will get the $y$coordinate Plugging 3 for $x$ into $y=x^26x$ gives $y=(3)^26(3)$ → $y=918$ → $y=9$
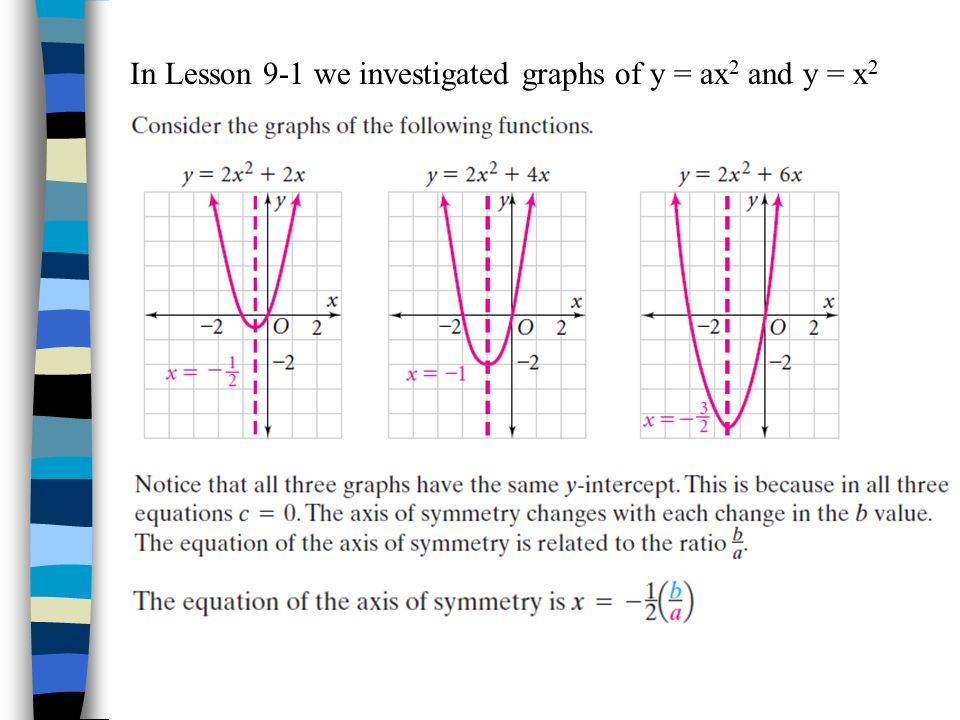
From eqations (4)and (5) we get a= 3 and b= 2 at last c=5 so the equation of parabola in the form y=ax^2byc will be y= 3x^2 2x5 Note the equation of above parabola in standard form is (x1/3)^2= 1/3(y 16/3) The prabola has a point Max ( 1/3 ;Examples ax^2bxc=0 x^2x6=9 x^2x6=0 x^21=0 x^22x1=3x10 2x^24x6=0 quadraticequationcalculator ax^2bxc=0 To calculate the axis of symmetry for a 2nd order polynomial in the form ax 2 bx c (a parabola), use the basic formula x = b / 2a In the example above, a = 2 b = 3, and c = 1 Insert these values into your formula, and you will get x = 3 / 2 (2) = 3/4 Write down the equation of the axis of symmetry



Find A Quadratic Function Y Ax 2 Bx C Mathskey Com




The Parabola Y Ax 2 Bx C Is Graphed Below Find A B C The Grid Lines Are One Unit Brainly Com
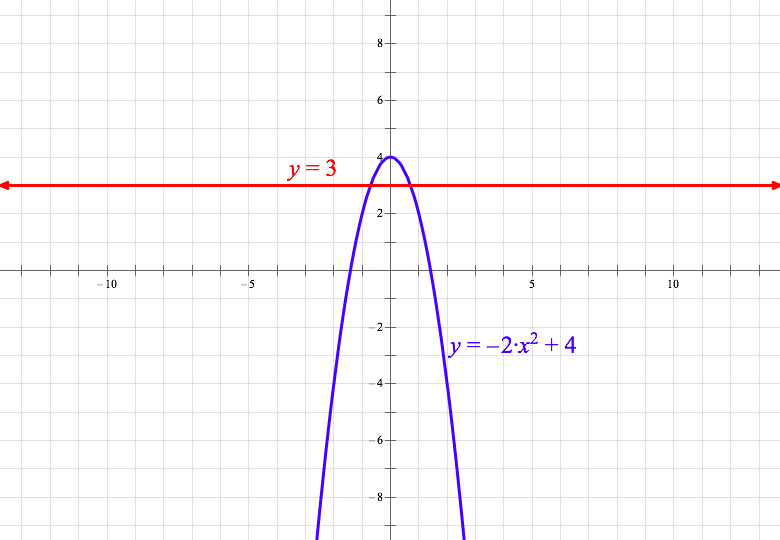
Y = ax 2 bx c In this exercise, we will be exploring parabolic graphs of the form y = ax 2 bx c, where a, b, and c are rational numbers In particular, we will examine what happens to the graph as we fix 2 of the values for a, b, or c, and vary the third We have split it up into three parts varying a only varying b only varying c only (2 , 1) >The standard form of )color(black)(y=ax^2 bx c)color(white)(a/a)))) The function here y = x^2 4x 3 " is in this form " with )color(black)((b)/(2a)color(white)(a/a)))) rArr x_(vertex) = (4)/(2) = 2 To find corresponding value of ycoord of vertex , substitute x = 2 into the function x = 2 y = (2)^2 4(2Equation y = 5x 2 Plotting these points and joining with a smooth curve gives Again, notice how the graph is symmetrical !



Solution A Quadratic Graph Has Maximum Point 2 5 And Passes Through Point 0 3 Find The Equation For The Graph In The Form Y Ax 2 Bx C




Y Ax 2 B N Find Dy Dx Maths Trigonometric Functions Meritnation Com
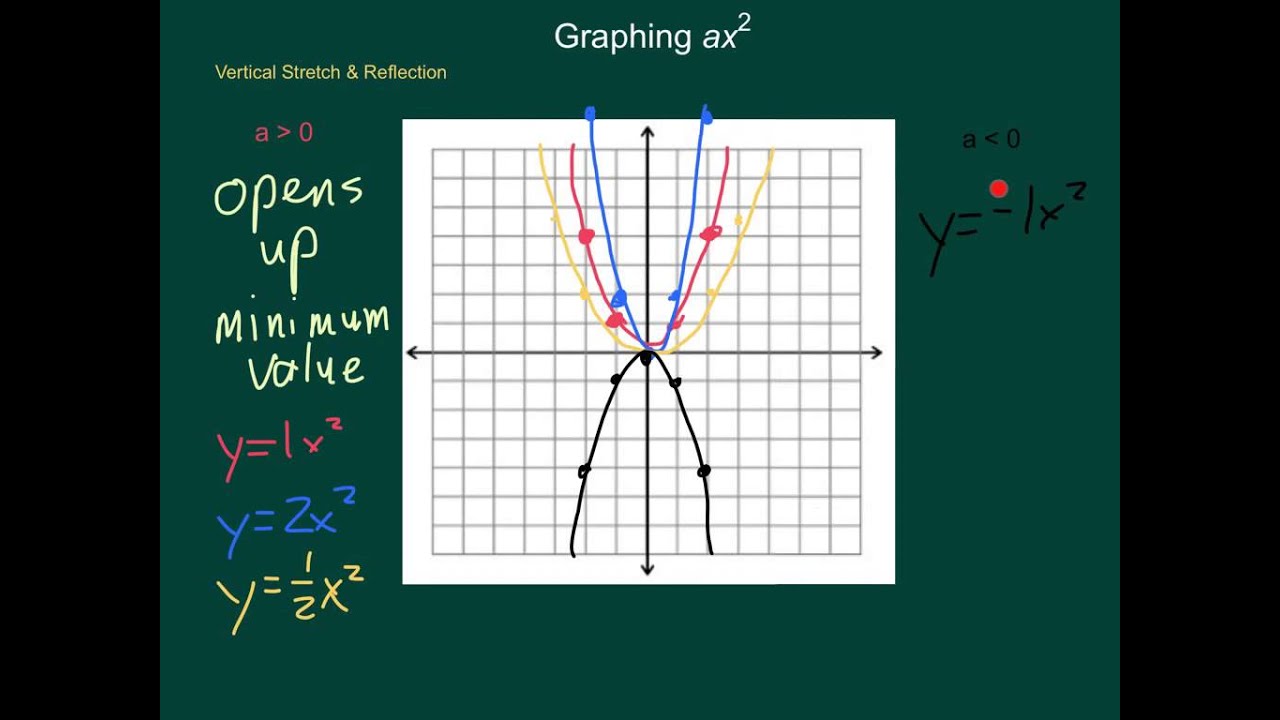
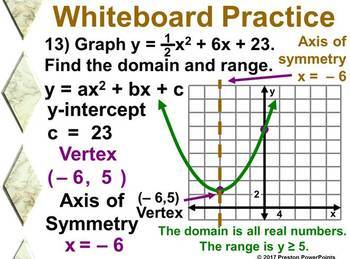
The graph of a quadratic function is a parabola The parabola can either be in "legs up" or "legs down" orientation We know that a quadratic equation will be in the form y = ax 2 bx cClick here👆to get an answer to your question ️ Find the degree of homogeneity of function f(x, y) = ax^2/3 hx^1/3 y^1/3 by^2/3 The formula for the axis of symmetry and the xcoordinate of the vertex is x=(b)/(2a) To find the ycoordinate of the vertex, substitute the value for x into the equation and solve for y y=a((b)/(2a))^2b((b)/(2a))c Example Find the vertex of y=x^2
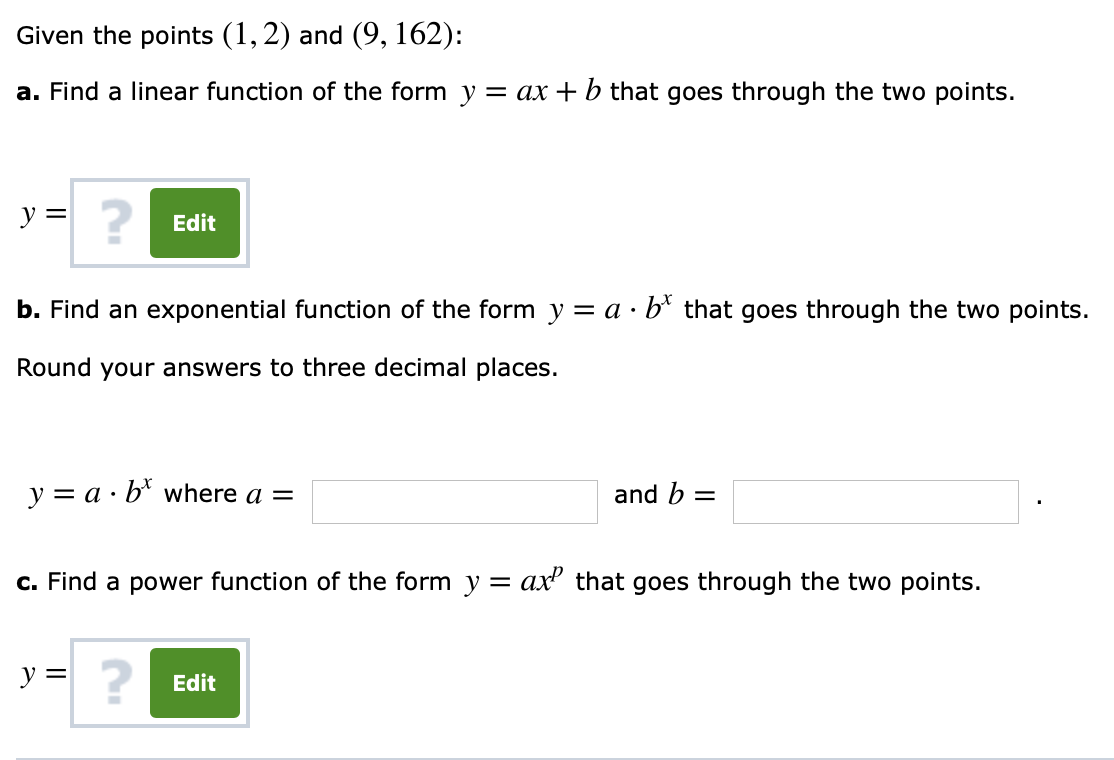



Answered Given The Points 1 2 And 9 162 A Bartleby




The Tangent For Math Y Ax 2 Bx 2 Math Goes Through Math 1 Frac 1 2 Math Which Is Also Parallel To The Normal Of The Curve Look Below Quora
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe yintercept is located at the point (0, c) The solutions of the quadratic equation ax 2 bx c = 0 correspond to the roots of the function f(x) = ax 2 bx c, since they are the values of x y = ax 2 bx c where a, b and c are known constants and x and y are variables Vertex form looks like this y = a(x b) 2 c where a, b and c are known constants and x and y are variables Factored form looks like this y = a(x r 1)(x r 2) where a is a known constant, r 1 and r 2 are "roots" of the equation (x intercepts), and x and y




Graphing Y Ax 2 Bx C




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download
Arguably, y = x^2 is the simplest of quadratic functions In this exploration, we will examine how making changes to the equation affects the graph of the function We will begin by adding a coefficient to x^2 The movie clip below animates the graph of y = nx^2 as n changes between 10 and 10 As you can see in the animation, the value of nFind in the form y= ax^2 bx c, the equation of the quadratic whose graph a) touches the xaxis at 4 and passes through (2,12) b) has vertex (4,1) andProperties A linear function is a polynomial function in which the variable x has degree at most one f ( x ) = a x b {\displaystyle f (x)=axb} Such a function is called linear because its graph, the set of all points ( x , f ( x ) ) {\displaystyle (x,f (x))} in the Cartesian plane, is a line The coefficient a is called the slope of the




54 The Graph Of Y Ax2 Bx C Is Shown In The Given Figu Scholr
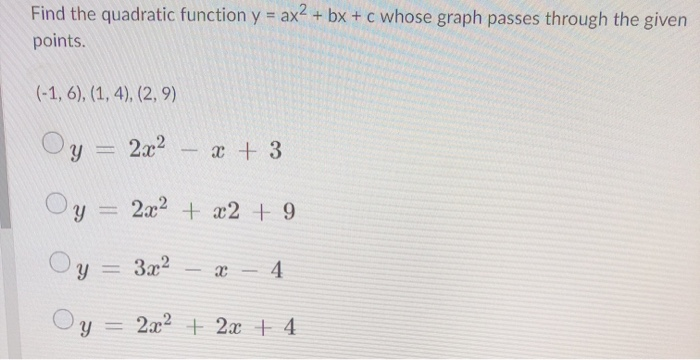



Find The Quadratic Function Y Ax2 Bx C Whose Chegg Com
Find the slope of the line with equation 3x 2y = 8 In order to find the slope, it is simplest to put this line equation into slopeintercept form If I rearrange this line to be in the form " y = mx b ", it will be easy to read off the slope m So I'll solve 3 x 2 y = 8 2 y = –3 x 8 y = − 3 2 x 4Step 2 calculate the \(y\)coordinate of the vertex, \(k\), by replacing \(x\) inside \(y=ax^2bxc\) and calculating the value of \(y\) Tutorial Coordinates of the Vertex In the following tutorial we learn how to find the coordinates of a parabola's vertex , in other words the coordinates of its maximum, or minimum, pointAnd if I drop b from equation and try to find out matrix A only y = Ax when vectors y and x (2x1) are known and matrix A (2x2) is unknown, how I can do that?




1 The Standard Form Of A Quadratic Equation Is Y Ax 2 Bx C 2 The Graph Of A Quadratic Equation Is A Parabola 3 When A Is Positive The Graph Opens Ppt Download



Quadratic Function Y Ax 2 Q Geogebra
Graph of y=ax^2k Graph of Try varying the values of k and a and see how it affects the graph of this quadratic function Write down what you see as you change each value of 'a' and 'k' Explain why?Click here👆to get an answer to your question ️ The graphs of y = ax^2 bx c are given in Figure Identify the signs of a, b and c in each of the following Join / Login Question The graphs of y = a x 2 b x c are given in Figure Identify the signs of a, b and c in each of the following HardStart with (x−4)2 (y−2)2 = 25 Move (x−4) 2 to the right (y−2)2 = 25 − (x−4)2 Take the square root (y−2) = ± √ 25 − (x−4)2 (notice the ± "plus/minus" there can be two square roots!) Move the "−2" to the right y = 2 ± √ 25 − (x−4)2 So when



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




Find The Length Of The Curve Y Ax 2 From X 0 To X 14 Where A Greater Than 0 Is A Real Number Set Up The Integral That Gives
Because I can't take inverse of x matrices vectorspaces transformation matrixequations affinegeometry Share Cite FollowA is the coefficient of the x^2 term In a straight line, the standard form of the equation is ax by = c where a is the coefficient of the x term b is the coefficient of the y term c is the constant term the slopeintercept form of the equation of a straight line is y = mx b where m is the slope b is the y How to Find the the Directionthe Graph Opens Towards y = ax2 bx c Our graph is a parabola so it will look like or In our formula y = ax2 bx c, if the a stands for a number over 0 (positive number) then the parabola opens upward, if it stands for a number under 0 (negative number) then it opens downward 6
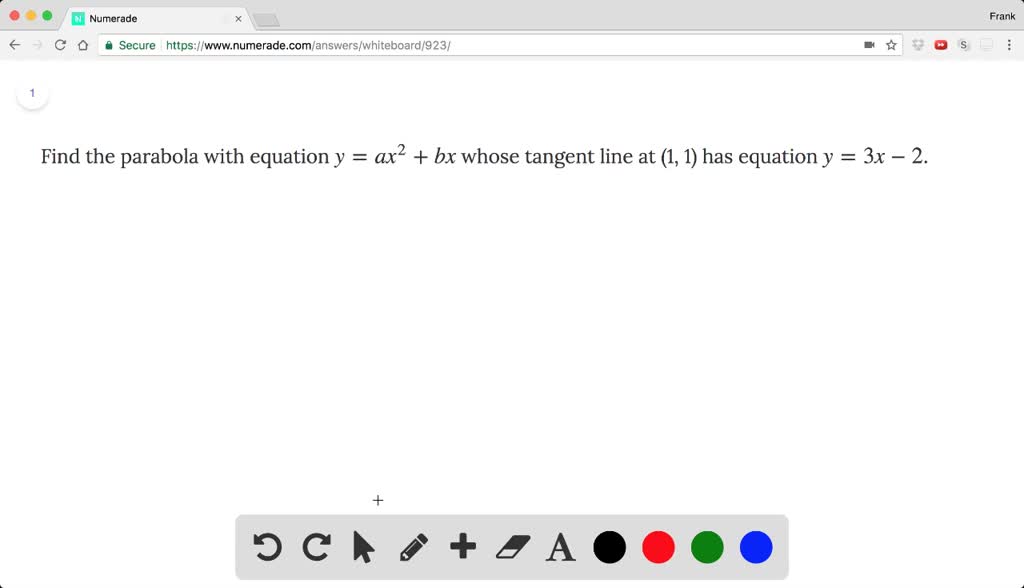



Solved Find The Parabola With Equation Y Ax 2
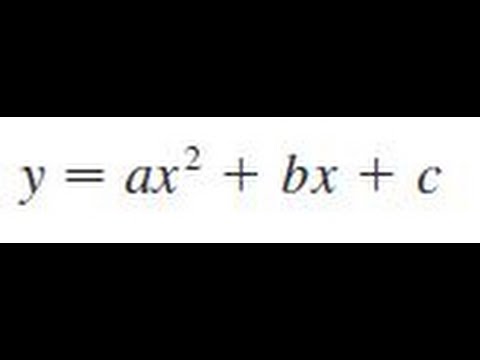



Differentiate The Function Y Ax 2 Bx C Youtube
Of that vague equation, the X coordinate is at b/2a To find the Y coordinate, plug it back in Now if you would like to do this the calculus way, differentiate the equation, and set the resulting 2ax = b and solve for X Then, plug the X backBut it all means the same thing, just different letters Slope (Gradient) of a Straight Line Y Intercept of a Straight Line Test Yourself Explore the Straight Line Graph Straight Line Graph Calculator Graph IndexY = kx n In your country let us know!



How To Determine A Quadratic Function Y Ax 2 Bx C If Its Graph Passes Through The Point 2 19 And It Has A Horizontal Tangent At 1 8 Quora



Unique Quadratic Equation In The Form Y Ax 2 Bx C
1 ax = 2/ x = 1/a Is there anything wrong?The solution looks like y= y c y p where y c is the complementary solution to the homogeneous DE ay00 by0 cy= 0 and y p is the particular solution To nd the particular solution using the Method of Undetermined Coe cients, we rst make The formula y = mx b is an algebra classic It represents a linear equation, the graph of which, as the name suggests, is a straight line on the x , y coordinate system Often, however, an equation that can ultimately be represented in this form appears in disguise




Find The Center Of Mass Of The Area Of The Xy Plane Bounded By The Parabola Y Ax 2 And The Line Y B The Area Has A Mass M Study Com




Ch 4 Pre Test 1 Graph The Function Y 4x 2 Then Label The Vertex And Axis Of Symmetry 2 Write The Quadratic Function In Standard Form Y X Ppt Download
1 Answer The quadratic equation y = ax 2 bx c The above function passes through the points (1,3), (3,1) and (4,0) Solve (1) and (2) to eliminate c variable and obtain two variable equation Solve (2) and (3) to eliminate c variable and obtain two variable equation Solve (4) and (5) to eliminate b variable and obtain one variableFinding y p in ConstantCoe cient Nonhomogenous Linear DEs Introduction and procedure When solving DEs of the form ay00 by0 cy= g(x);Y = ax q y = a(x p)2 q y = abxp q b > 0,b ≠ 1 a y = q x p a > 0 a > 0 51 STRAIGHT LINE General representation or equation y = ax q or y = mx x a or m is the gradient and q or c is the y intercept Also note the shape of the following linear functions a < 0 a = 0 a > 0 a is undened




Solved In Exercises 19 22 Find The Quadratic Function Y A X 2 B X C Whose Graph Passes Through The Given Points 2




Y Ax2 Bx C Solution
If you don't see an x 2 term, you don't have a quadratic equation!To make y=12x32 look like ax 2 bxc, you need to make a=0, b=12, c=32 But 'a' can't be zero in standard quadratic form, since 'a'=0 turns the equation into a linear equation!Answer to Find the quadratic function y = ax^{2} bx c whose graph passes through the given points (2,0), (1,0), and (3,10) By signing up,



Pwn Test Prep Sat Q A Satpracticetest2 Qn 29 Y 3 Y Ax 2 B In




Quadratic Function Y Ax 2 Bx C Quadratic
A x 4 b x 2 c = 0, ax^4 bx^2 c = 0, ax4 bx2 c = 0, can be made much simpler by the substitution u = x 2 u = x^2 u = x2 So the equation becomes a u 2 b u c = 0, au^2 bu c = 0, au2 bu c = 0, a quadratic, which of course is much easier to solve For the solution, you can either factor it expicitlyY = Ax where A ∈ Rm×n is fat (m < n), ie, • there are more variables than equations • x is underspecified, ie, many choices of x lead to the same y we'll assume that A is full rank (m), so for each y ∈ Rm, there is a solution set of all solutions has formCalculus Find dy/db y= (axb)^2 y = (ax b)2 y = ( a x b) 2 Differentiate both sides of the equation d db(y) = d db((axb)2) d d b ( y) = d d b ( ( a x b) 2) The derivative of y y with respect to b b is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps



Mathematics Upper Secondary Ydp Student Activity The Functions Y Ax 2 Q




Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt
Find the yintercept The yintercept of any graph is a point on the yaxis and therefore has xcoordinate 0 We can use this fact to find the yintercepts by simply plugging 0 for x in the original equation and simplifying Notice that if we plug in 0 for x we get y = a(0) 2 b(0) c or y = c So the yintercept of any parabola is always at (0,c)Find stepbystep Algebra solutions and your answer to the following textbook question Find a and b if the graph of $$ y = ax^2 bx^3 $$ is symmetric with respect to the origin (There are many correct answers)For more problems and solutions visit http//wwwmathplanetcom




Graphing Quadratic Functions Y Ax 2 Bx C




Quadratic Equations Tutorial



Q Tbn And9gcskitjvtu4g6u7oh5r8z42jlb391urt3idlmfdbjguuxli7v2fo Usqp Cau



Quadratics



Solution Solve The Exercise By Solving A System Of Equations Find The Quadratic Equation Of The Form Y Ax 2 Bx C Whose Graph Passes Through The Points 2 4 2 8 And 1 4




The Graph Of The Quadratic Function Y Ax 2 Bx C Is Given Find A B C Brainly Com
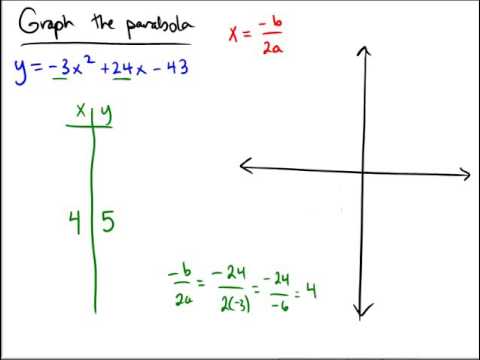



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube



Quadratics




Quadratic Function Y Ax 2 Bx C Quadratic



1




Is There A Formula For Finding The Translations Regarding Y Ax B X Askmath
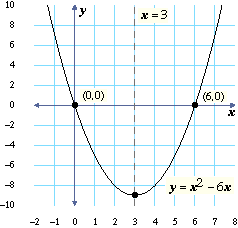



Investigating Y Ax 2 Bx



Quadratic Function




3 Ways To Find The Inverse Of A Quadratic Function Wikihow
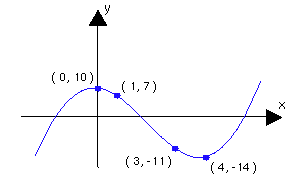



Linear Algebra Webnotes Class Assignments Chapter 1



Quadratics




Example 3 Graph A Function Of The Form Y Ax 2 Bx C Graph Y 2x 2 8x 6 Solution Identify The Coefficients Of The Function The Coefficients Ppt Download



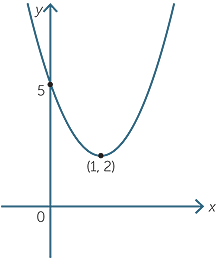
Quadratic Graph Example Y Ax C Expii




Answered Given The Points 1 2 And 8 128 A Bartleby




Graphing Y Ax 2 C
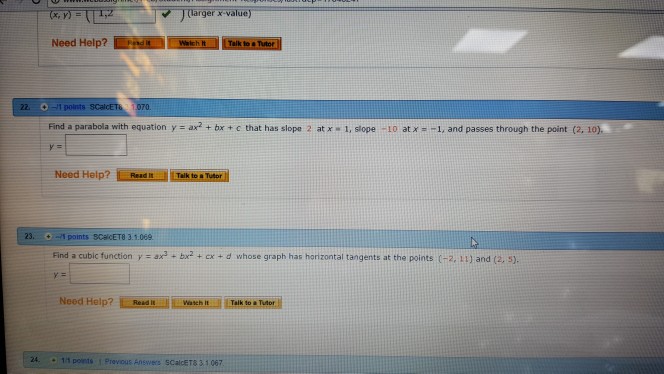



Arger X Value 22 1 Pants Find A Parabola With Chegg Com




Finding The Inverse Of Y Ax2 Bx C By Completing The Square Youtube
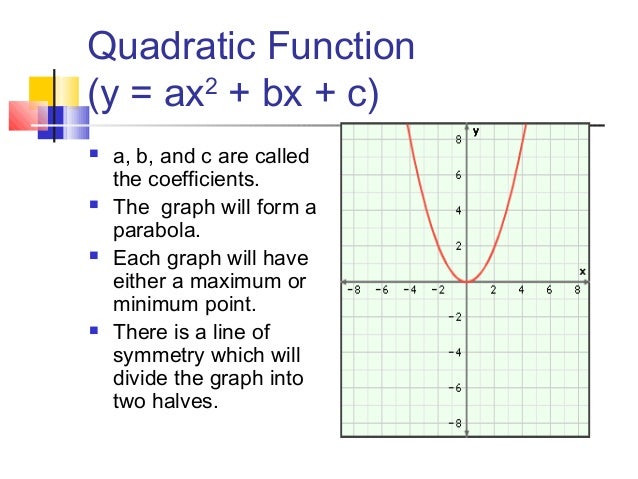



5 1 Quadratic Functions
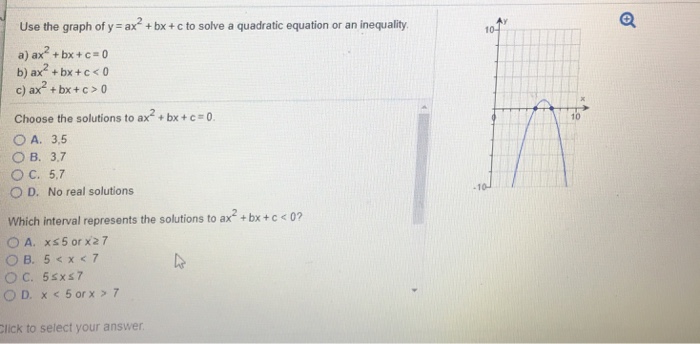



Use The Graph Of Y Ax 2 Bx C To Solve A Chegg Com
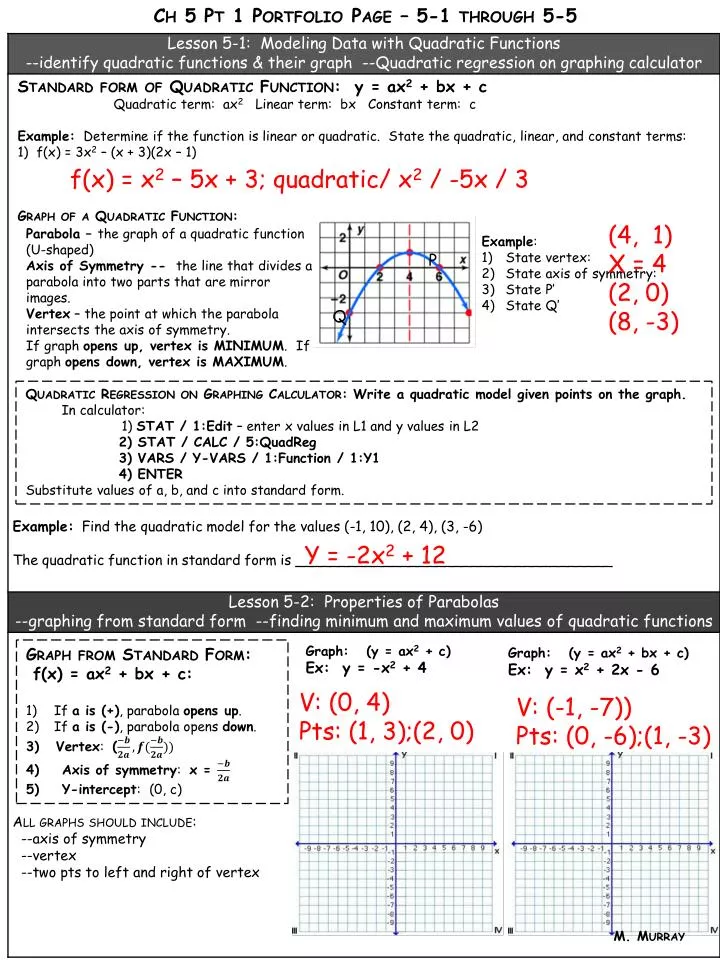



Ppt Standard Form Of Quadratic Function Y Ax 2 Bx C Powerpoint Presentation Id




How Do You Find The Axis Of Symmetry For A Quadratic Function Printable Summary Virtual Nerd




Unit 7 Quadratic Relations Of The Form Y Ax 2 Bx C Pdf Free Download



A Tangent To A Quadratic




The Tangent To Y Ax 2 Bx C At 1 2 Is Parallel To The Normal At The Point 2 2 On The Youtube



Solution Find The Values Of A B And C Such That The Equation Y Ax2 Bx C Has Ordered Pair Solutions 3 23 1 9 And 3 5
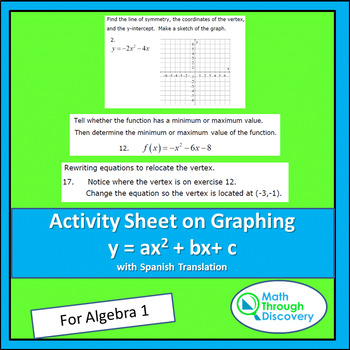



Algebra 1 Activity Sheet On Graphing Y Ax 2 Bx C Tpt




Refer The Picture Also Y Ax 2 Bx C Hd Png Download Transparent Png Image Pngitem




Quadratic Function Y Ax 2 Bx C Quadratic



Untitled Document




1 Point The Equation For A Parabola Has The Form Y Ax2 Bx Cy Ax2 Bx C Where And Cc Are Brainly Com
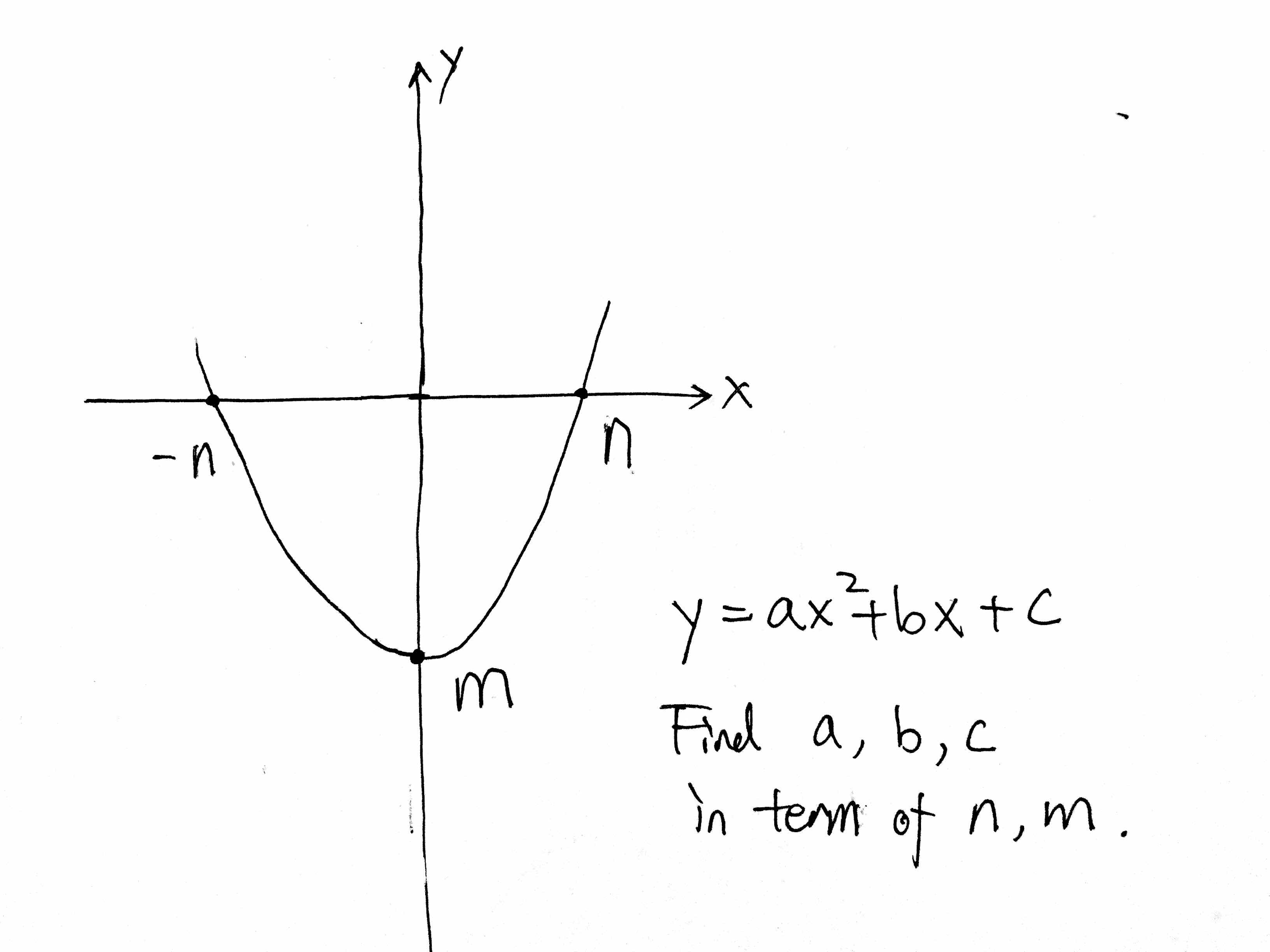



Y Ax 2 Bx C Find A B C In Term Of N M Chegg Com



Exploring Parabolas Y Ax 2 Bx C




If The Curve Y Ax 2 Bx C Passes Through The Point 1 2 And The Line Y X Touches Youtube
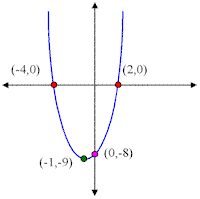



Parabolas



Quadratic Function Y Ax2 Bx C When A Is Sutori



What Are The Coefficients A B And C Of The Parabola Y Ax 2 Bx C That Passes Through The Point 3 13 And Tangent To The Line 8x Y 15 At 2 1 Quora



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
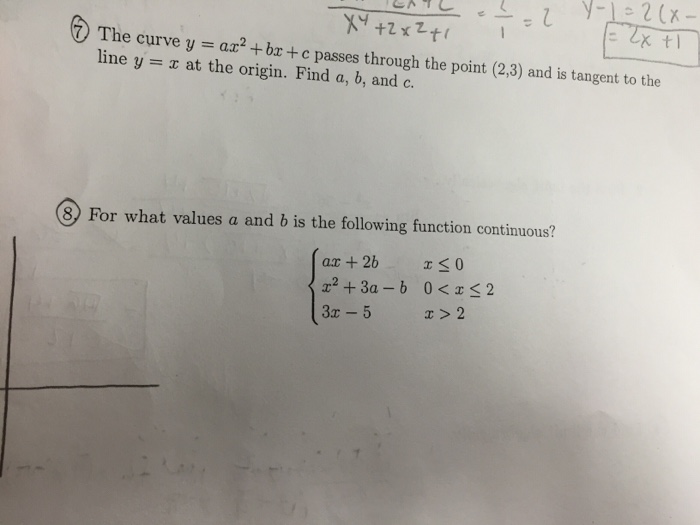



The Curve Y Ax 2 Bx C Passes Through The Point Chegg Com
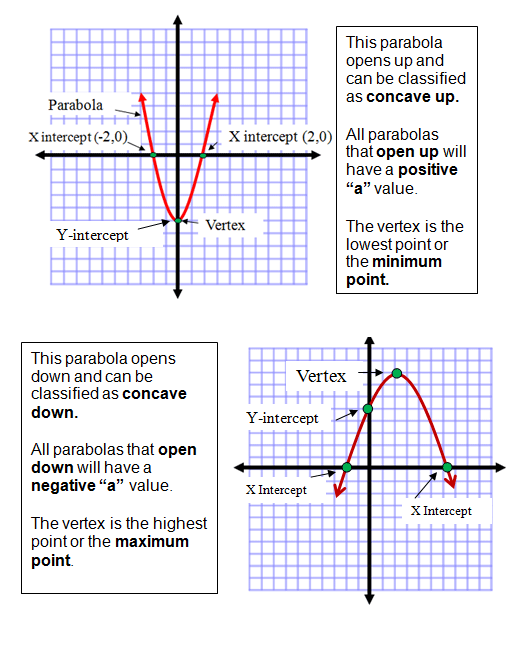



Graphing Quadratic Equations




Y Ax 2




Y Ax Bx C



Www Shsu Edu Kws006 Precalculus 2 1 Quadratic Functions Files S 26z 2 3 Pdf
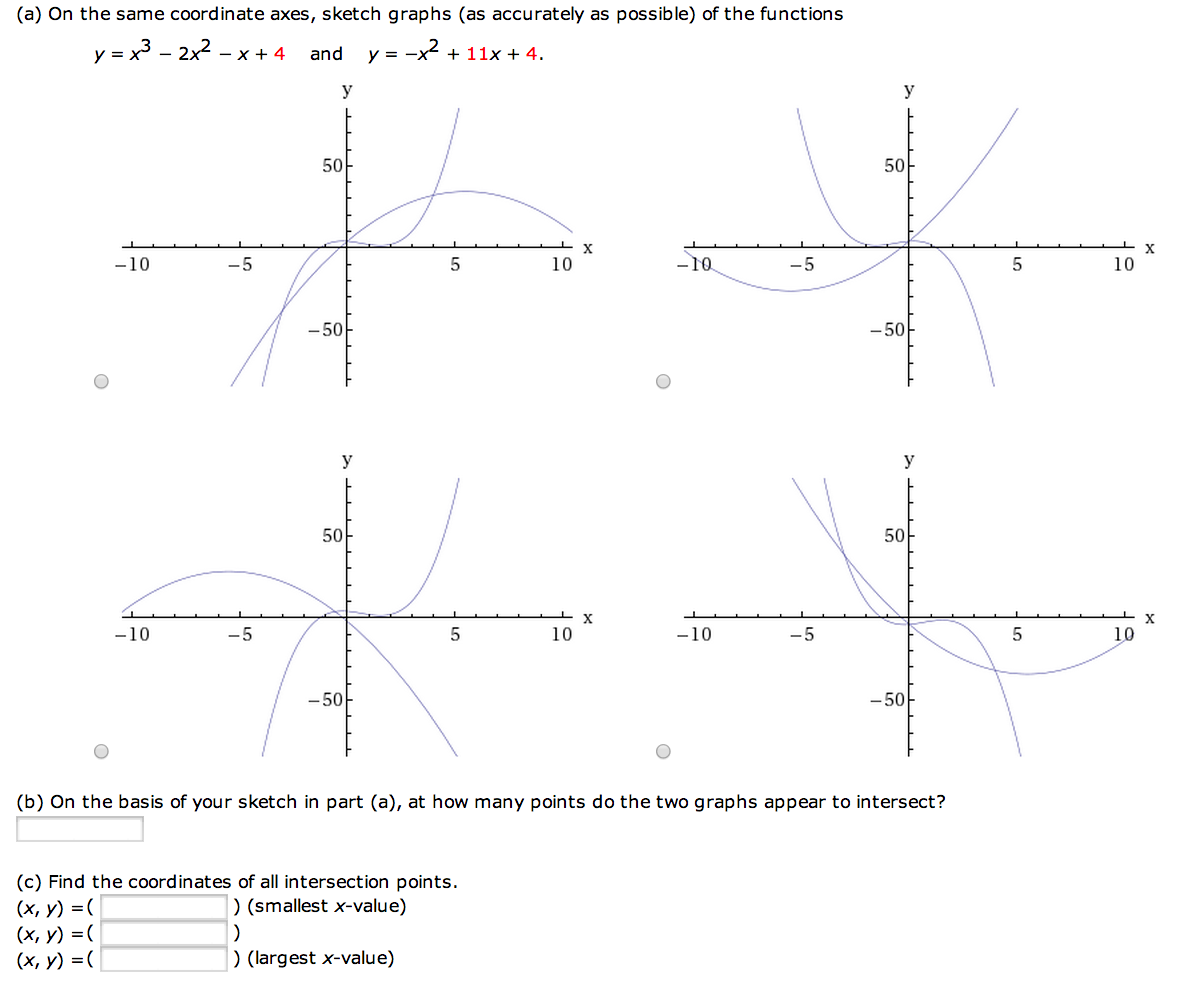



Find A Parabola With Equation Y Ax2 Bx C That Chegg Com



1




If The Curve Y Ax 2 Bx C Passes Through The Point 1 2 And The Line Y X Touches It At The Origin Then
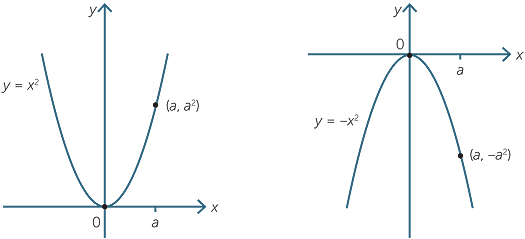



Quadratic Function
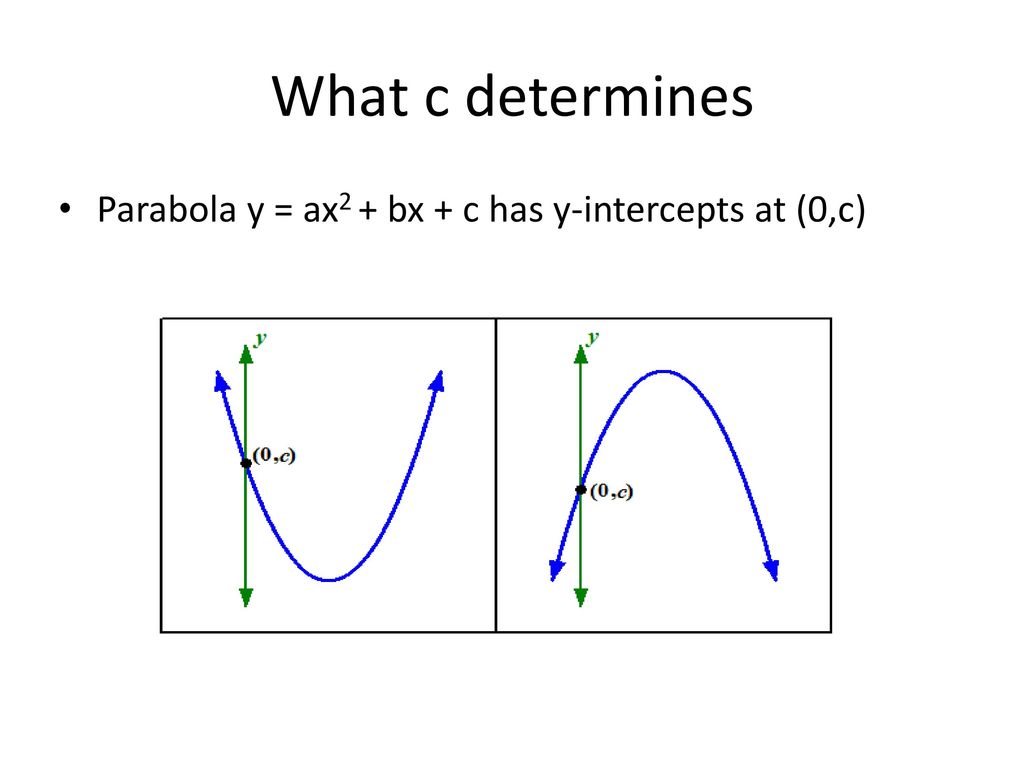



How To Draw A Parabola Ppt Download




The Tangent To Y Ax 2 Bx 7 2 At 1 2 Is Parallel To The Normal At The Point 2 2 On The Curve Y X 2 6x 10 Find The Value Of A And B



Algebra1 Graphing Y Ax 2 Youtube




8 4 Graphs Of Quadratic Equations And Functions




Sketching Graphs Of The Form Y Ax2 Q Functions I



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id




Myn Find An Equation Of The Parabola Y Ax2 Bx C Th Gauthmath




Missing C Value Quadratics




Graphing Y Ax 2 C




Ppt Graphing General Quadratics Y Ax 2 Bx C Powerpoint Presentation Id



Lesson 9 2 Graphing Y Ax Bx C Objective To Graph Equations Of The Form F X Ax Bx C And Interpret These Graphs Ppt Download
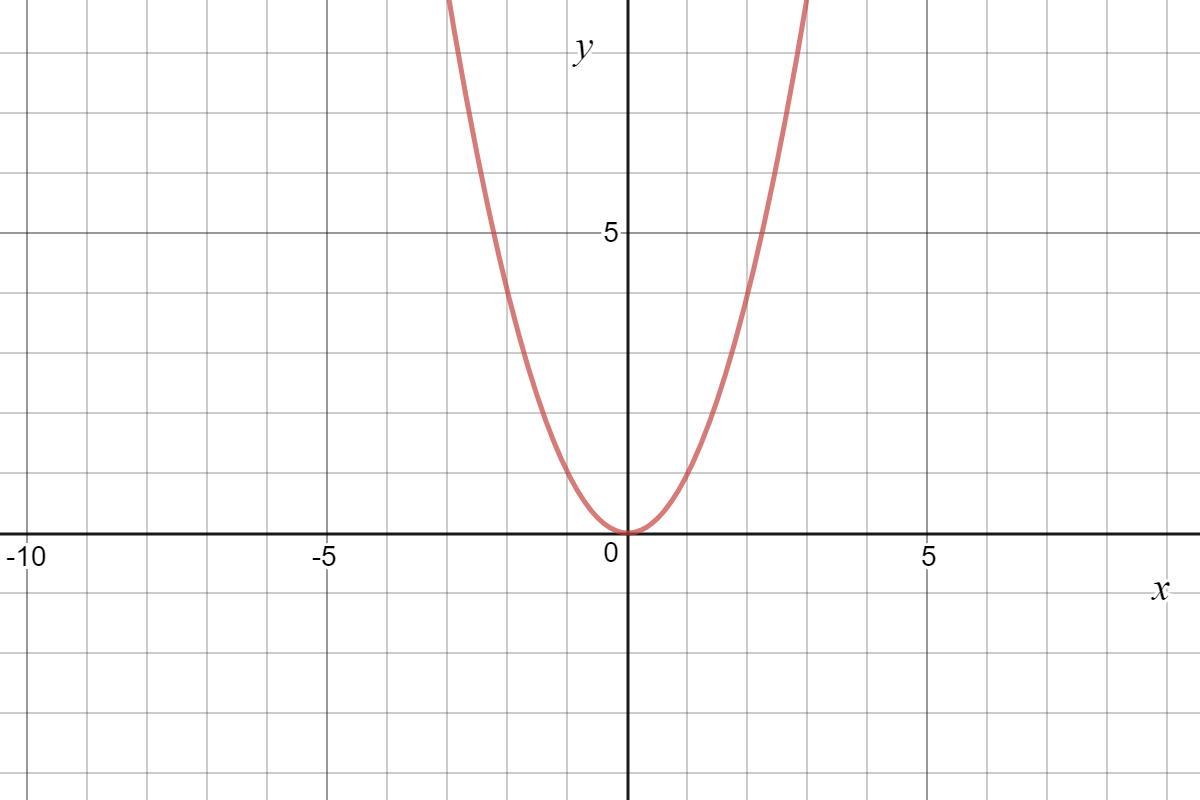



Quadratic Graph Example Y Ax C Expii



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora
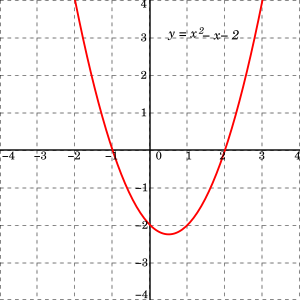



Quadratic Equation Wikipedia




Graphing Y Ax 2 C



Quadratics
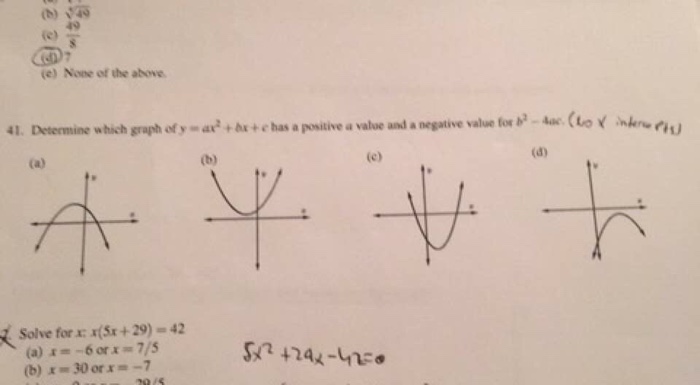



Determine Which Graph Of Y Ax 2 Bx C Has A Chegg Com




Graphing Quadratic Functions Y Ax 2 Bx C




Find The Equation Of A Cubic Curve In The Form Y Ax 3 02 Vividmath Au
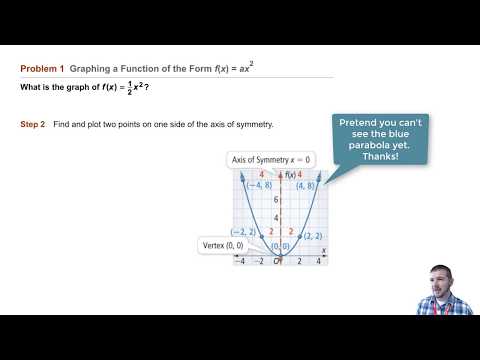



Quadratic Graph Example Y Ax Expii




View Question The Graph Of The Equation Y Ax 2 Bx C Where A B And C Are Constants Is A Parabola With Axis Of Symmetry X 3 Find B A



1
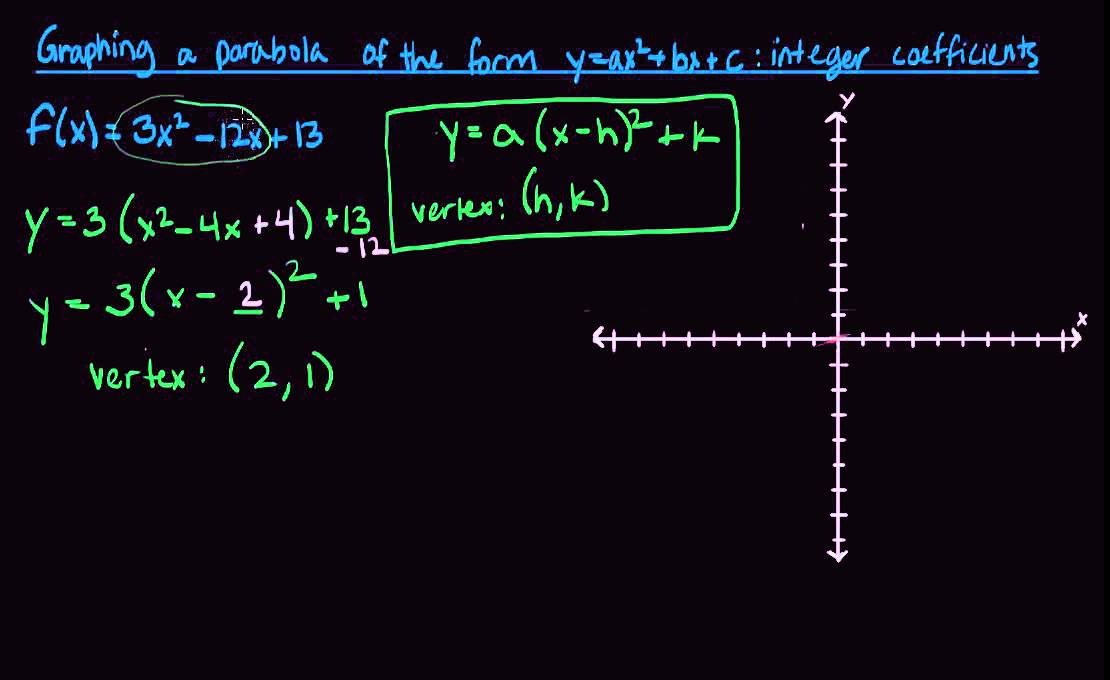



Graphing A Parabola Of The Form Y Ax2 Bx C With Integer Coefficients Youtube




Graphing Y Ax2 Bx C Youtube
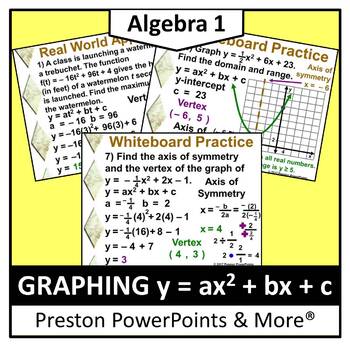



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt



Find The Parabola With Equation Y Ax 2 Bx Whose Tangent Line At 2 4 Has Equation Y 8x Brainly Com



0 件のコメント:
コメントを投稿