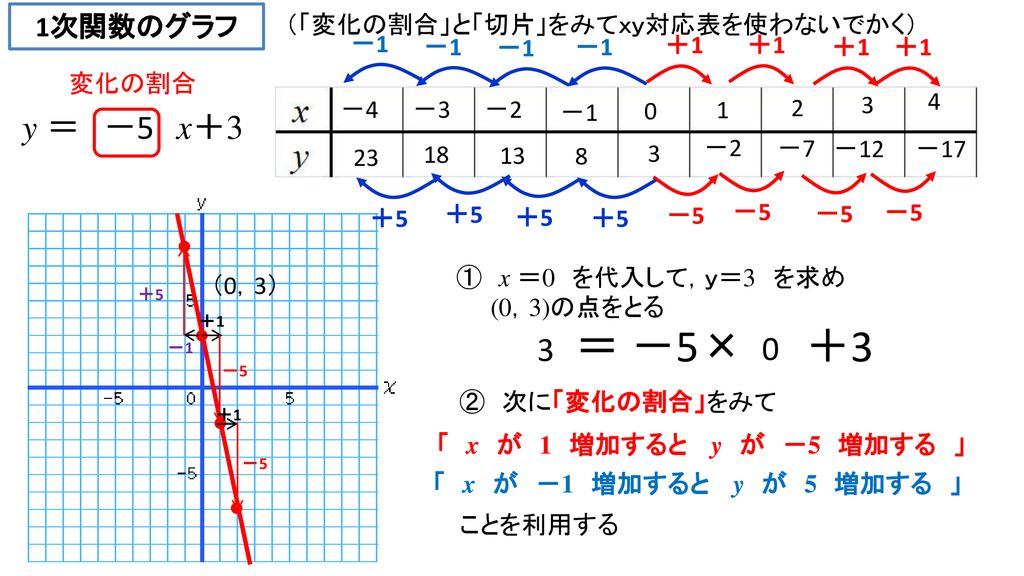
1次関数のグラフを効率よくかくた 引① 引③ 1次関数をグラフで表すよさは何で 鍛 鍛 8 グラフの傾きや切片, グラフが通る座標に着目 し,y=aχ+bの値と 関連付けて考えることを 通して,1次関数の式を 求める。 ・1次関数を求めるのに必要な条件下の表は,その結果と,手元に届いている5 つの教科書 会社の教科書の表記をまとめたものである. 学習指導要 領(解説) 二次関数 二元一次 不定方程式 二進法 s社 2次関数 1次不定 方程式 2進法 k社 2次関数 二元一次 不定方程式 二進法 t社 2次関数 2元1次 方程式 2進法 d社 2次関数 2元1次 方程式 二進法・1次関数による変域の対応関係を調べることができる。 ・いろいろな条件を満たす1次関数を求めることができる。 ・1次関数を使って、具体的な事象の問題を解決することができる。 〔表 現・処 理〕 ・1次関数を式や表、グラフで表すことができる。
中2数学 一次関数 一次関数 を大嫌いな人が最初に読む記事 たけのこ塾 勉強が苦手な中学生のやる気をのばす
1次関数 表
1次関数 表-二次関数 二次関数とそのグラフ 二次関数の値の変化 ・二次関数の最大・最小 ・二次方程式 ・二次不等式 データの分析 ・データの散らばり ・データの相関 場合の数と確率 場合の数 ・数え上げの原則 ・順列・組合せ 確率 ・確率とその基本的な法則1 1次関数に関する既習事項を整理し,表, 関1次関数で学習した表,式,グラフの特徴や変化の ( 式,グラフの相互関係や,1次関数の特割合の性質を関連付けてまとめようとする。 本時徴についての理
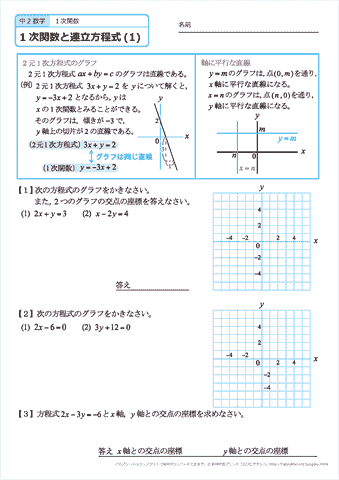



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
「1次関数の式」とは、 「y = a x b」 のことですよ! (3) y = a x b (← まずこう書く!) 点(4,1) とあるので、 x=4 、 y=1 を代入。 1=4 a+b 切片が9 とあるので、 b=9 を代入すると、 1=4 a+9 4 a=-8 a=-2(1)1次関数の変化の特徴 1次関数y=3x2について、次の表をうめてみましょう。そして、xの値が1増えるとき、 yの値がどのように変化するかを調べてみましょう。 x8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 y4 1 2 5 8(1)1次関数y=ax2で,xの増加量が2のとき,yの増加量は4である。 (2)1次関数y=2ax3で,xの増加量が3のとき,yの増加量は−12である。 (3)1次関数y=3ax2で,xの値が1から3まで増加するとき,yの値は8からまで 増加する。
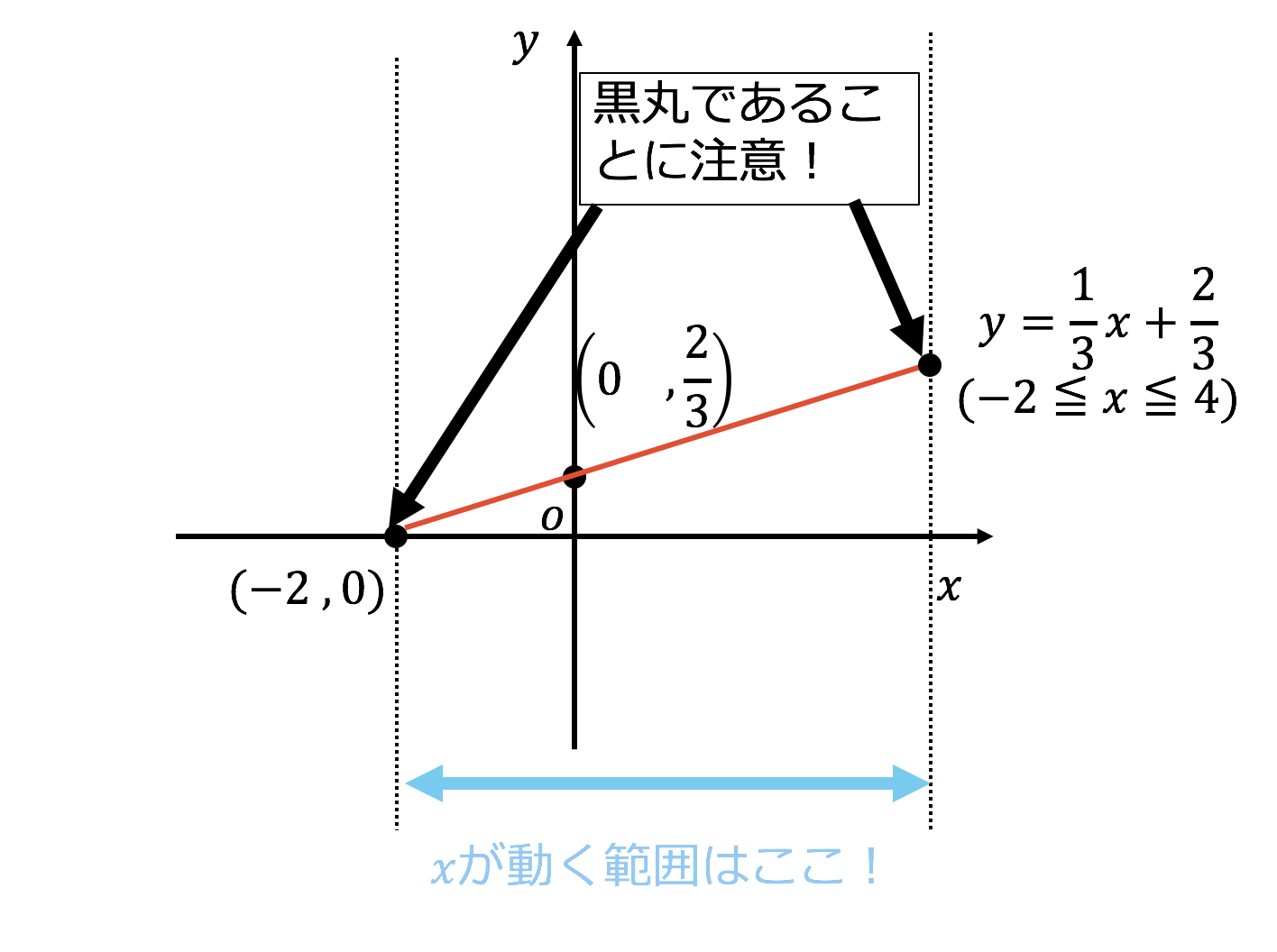
③\(\displaystyle{y=\frac{1}{2}x}\)はパッと見たところ、一次関数ではないように見えますがこれは\(a=\frac{1}{2}, b=0\) になっている一次関数の式です。 ④\(y4=2x^2\) は式を変形して、\(y=2x^24\) の形にすると\(x\)が二乗になっていて、二次式になっていることが傾きと1点から1次関数の式を出す y = axb の傾きaとx, yに数字を代入してbを求める。 例傾き3で、x=1のときy=−2となる1次関数の式を求める。 傾きa=3 なので、 y=3xbNo1定着1次関数① 組 氏名 答 ① 16,15,14,13,11,10,9,8,7 イ 1ずつ減少する ウ y=-x+17 エ 1次関数といえる 問 長さcmのばねがあり,おもりをつるしていくとばねは一定の割合で伸びていきます。xgの おもりをつるしたときのばねの長さをycmとして下の表のような結果が得られたとき,次の各問
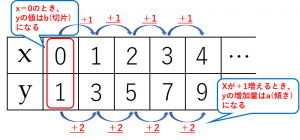
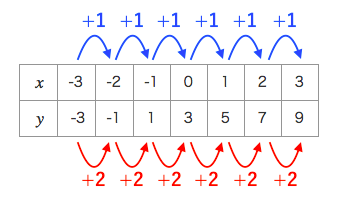
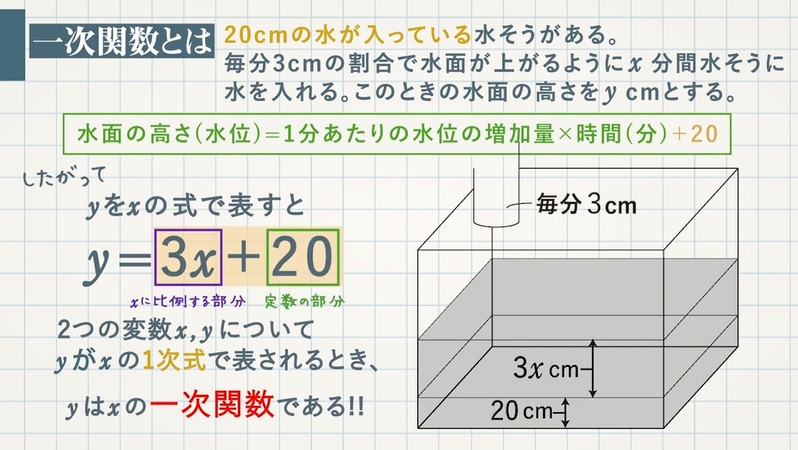
が の関数で、 が の 1次式 、 (、は定数、) の形で表せるとき、 は の「 1次関数 」であるといいます。 のときは になりますが、これも1次関数です。 1次関数の例 この1次関数では、 と の関係は表のようになります。 この表から、 が 増加するごとに比例も一次関数の一種ですが、比例の式に "定数項" が加わったものが一次関数です。 一次関数を表す式: 『y=ax b y = a x b 』①1次関数は「 y = a x b 」②「通る」と言ったら「代入成立」③傾きはyの増加量/xの増加量前の動画1次関数とグラフhttps//youtube/por9dOUBmHA次



3分で分かる 一次関数の意味 用語 グラフの書き方をわかりやすく 合格サプリ




一次関数 応用問題 中学生 数学のノート Clear
一次関数 式の求め方対応表が与えられる (9)対応する\(x、y\)の値が下の表のようになる一次関数 与えられた対応表から情報を読み取る必要があります。1次関数の表から変化の割合 作成者 nunokazu 表の中の青い点を動かすと、1番目のxの値 (x1)と2番目のxの値 (x2)を変えることができます。 その取り方を変えたときに、変化の割合の計算がどうなるかを観察しましょう。1次関数の表,式,グラフの関係についてまとめ る。 1次関数の増減とグラフの特徴についてまとめ る。 具体的な事象において,グラフの切片や傾きが何 を意味しているかを考える。 見 1次関数の表,式,グラフを,関連づけて考えることがで きる。



1次関数 1次関数の基礎とグラフ



一次関数の要点まとめ
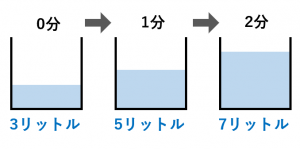
2 1次関数 =3 −2の と の対応表を見て, の値が1増えるときの の増加量を答えなさい。 3 次の1次関数の変化の割合を求めなさい。 4 1次関数 =2 +1において, の値が1から3まで増加するとき,次の問いに答えなさい。 (1) の増加量を求めなさい。・事象の中には1次関数として 捉えられるものがあることや 1次関数の表,式,グラフの 関連などを理解することがで きる。 お湯を沸かすときの時間と温度 の変化には1次関数y=aχ+ bという関係があることを見付 けたよ。 1次関数y=aχ+bの関係に1次関数とは、次数が1の関数のことです。 次数とは未知数の一番大きい指数が何乗なのかを表したものなので、未知数xの指数が1になっていれば1次関数となります。 したがって、次のような関数を1次関数といいます。 y=2x、y=5x、y=10x+7




1次関数 の勉強法のわからないを5分で解決 映像授業のtry It トライイット




対応表のxの求め方を教えて下さい Clear
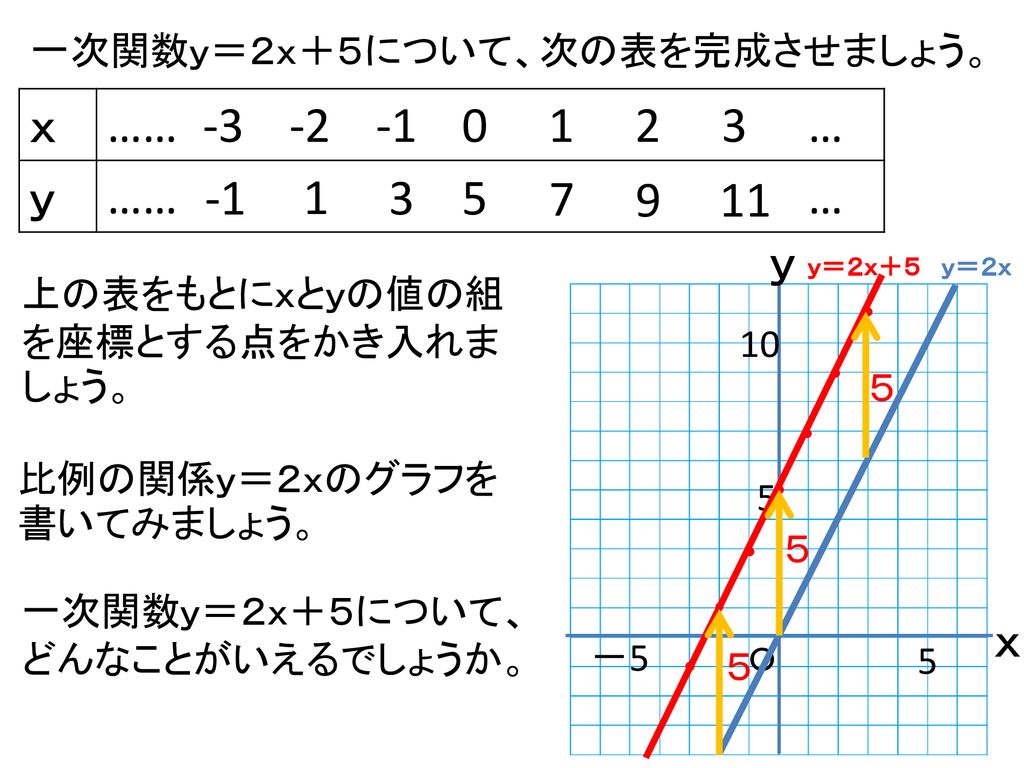
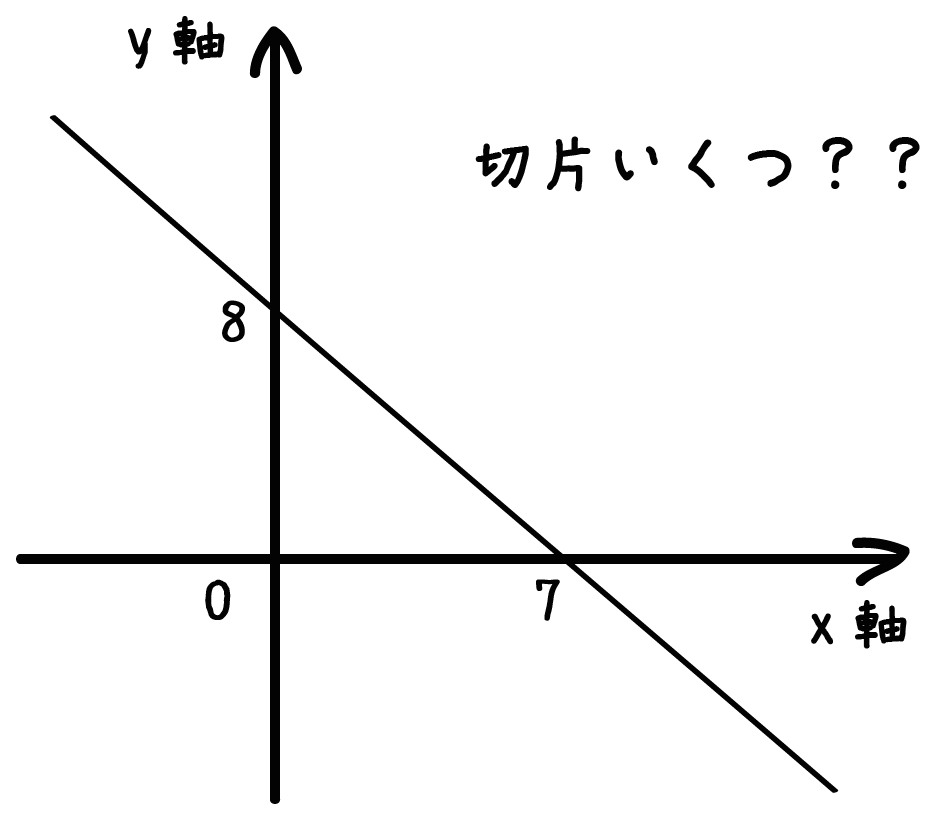
この頁の目標 1次関数のグラフを見て,方程式が答えられるようにする. i 直線のグラフから「切片」と「傾き」を読み取れるようにする. ii 直線のグラフから1次関数の方程式を答えられるようにする. iii 傾きが分数になるときでも,直線のグラフから1次関数の方程式を答えられるよう1次不等式を解く 10 6/14 1次方程式・1次不等式の応用 11 6/21 2次関数 関数 12 6/28 2 次関数の頂点 13 7/5 2 次関数のグラフをかく 14 7/12 21次関数の表 1次関数 y =2 x 1 で x の値を x =1に決めると y の値は y =2×1+1=3から y =3と決まります。 同じように x の値 x =2、 x =3、 x =4、と1つ決めるとそれに対応して y の値が y =5、 y =7、
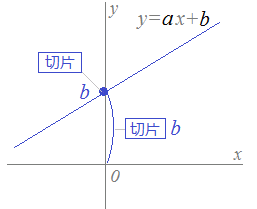



1次関数 グラフ 直線の方程式




一次関数の文章題 無料で使える中学学習プリント
y'' = 0 のとき \sin x = 0 、 0 \leq x \leq 2\pi より x = 0, \pi, 2\pi 0 \leq x < \pi で y'' < 0 \pi < x \leq 2\pi で y'' > 0 また、 x = 0 のとき y = 0 \displaystyle x = \frac {2} {3}\pi のとき \displaystyle y = \frac {2} {3}\pi \sqrt {3} ( \displaystyle \frac {2} {3}\pi \sqrt {3} ≒ \frac {2} {3} \cdot 314 173 = 38 )関数 ③ の増減表は次のようになる。 したがって,関数 ③ は で極小値 をとり,条件を満たす。 よって D ,Eまた, 1次関数のグラフを利用して,連立1 次方程式を解くには, 1次関数をみたすすべて の点(x, y)は一つの直線上にあり,逆にその直 線上のすべての点が1次関数をみたすというこ とを理解できていないと納得はできないだろ う。
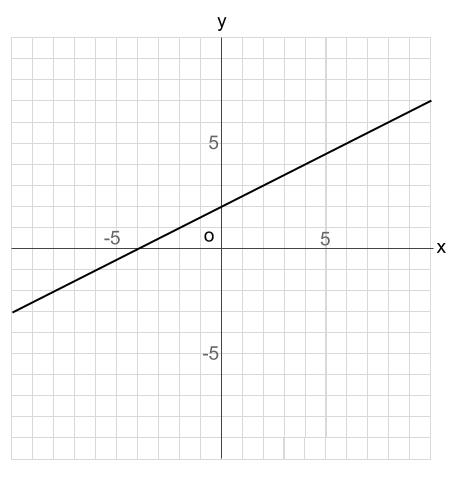



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
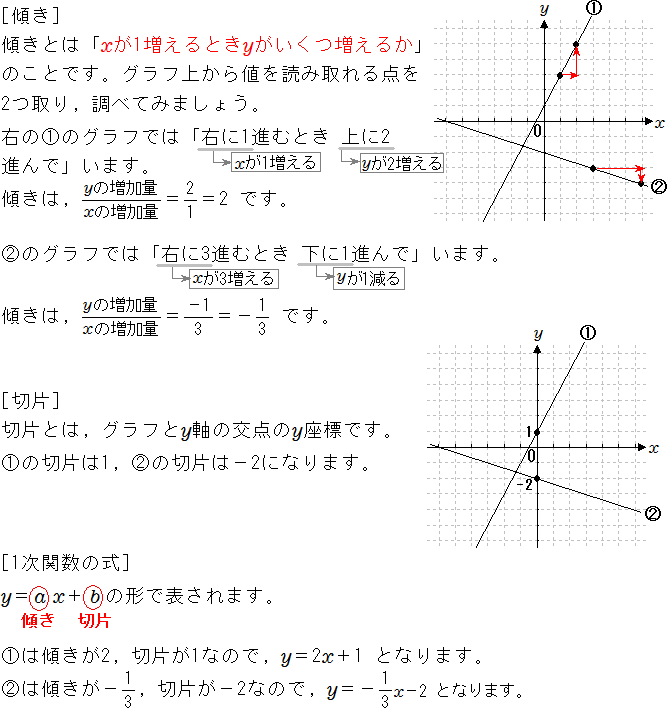



1次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト
Y 43n 0 増減表の作り方(要点) (1) y ' を求める. (2) y '=0 となる x の値を求める.==> x の方程式を解く. (3) y '=0 となる x の値を 区切り目 として表を書く. 上の行は x の値 、次の行は y ' の符号 、一番下の行は y の値 を表すものとして,表は上から例1はすべて関数の式であるが、 (a)と (c)は右辺がxの 1次式 になっている。 これを 1次関数 という。 さらに、1次関数のうち特に (a)のように定数項がない形のものが比例である (1年の範囲) 例1の (b)はxの2次式なので2次関数、 (d)は3次式なので3次関数である。C 関数 (1) 具体的な事象の中から二つの数量を取り出し,それらの変化や対応を調べることを通して,比例,反比例の関係についての理解を深めるとともに,関数関係を見いだし表現し考察する能力を培う。 ア 関数関係の意味を理解すること。
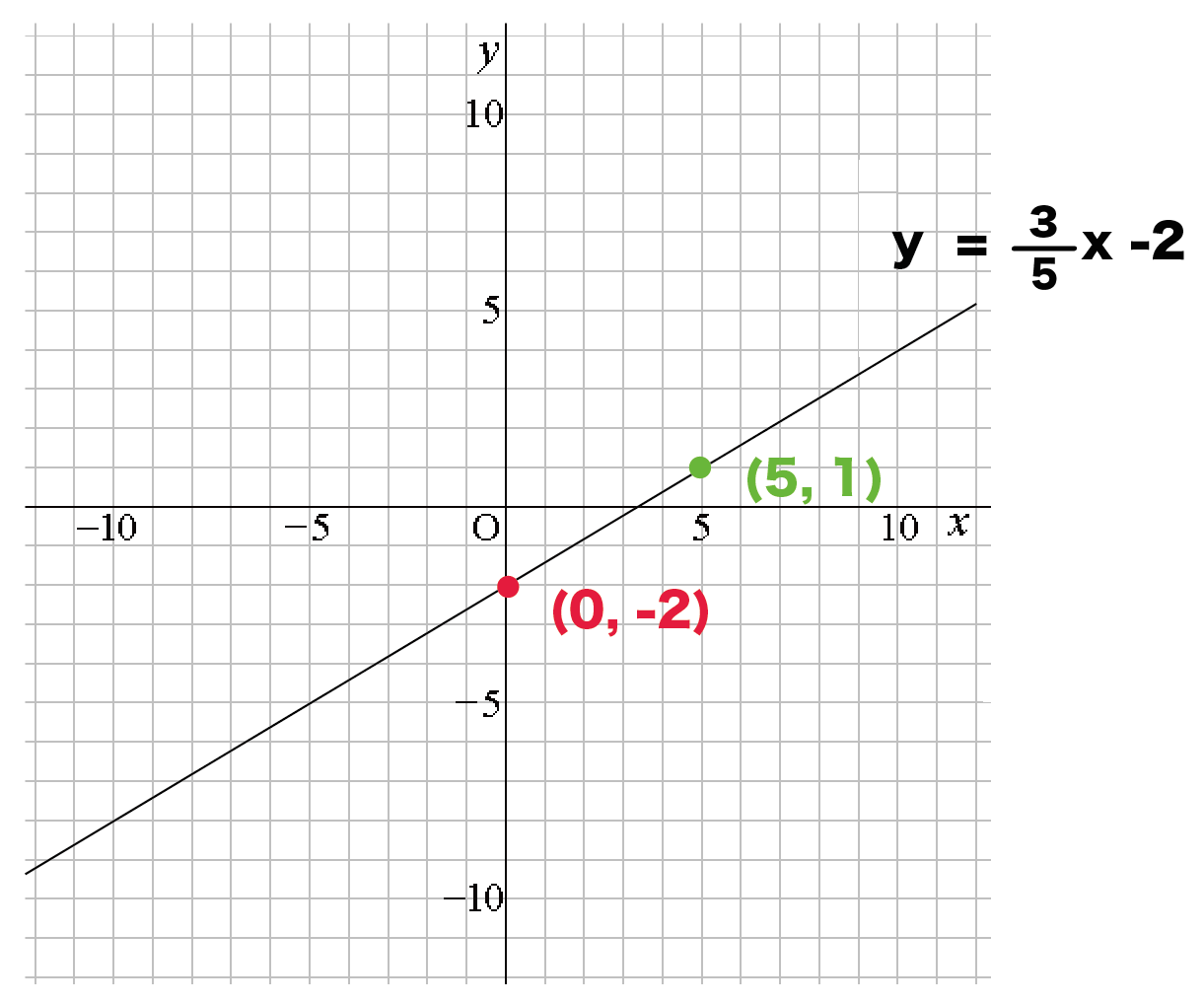



中2数学 一次関数のグラフの書き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
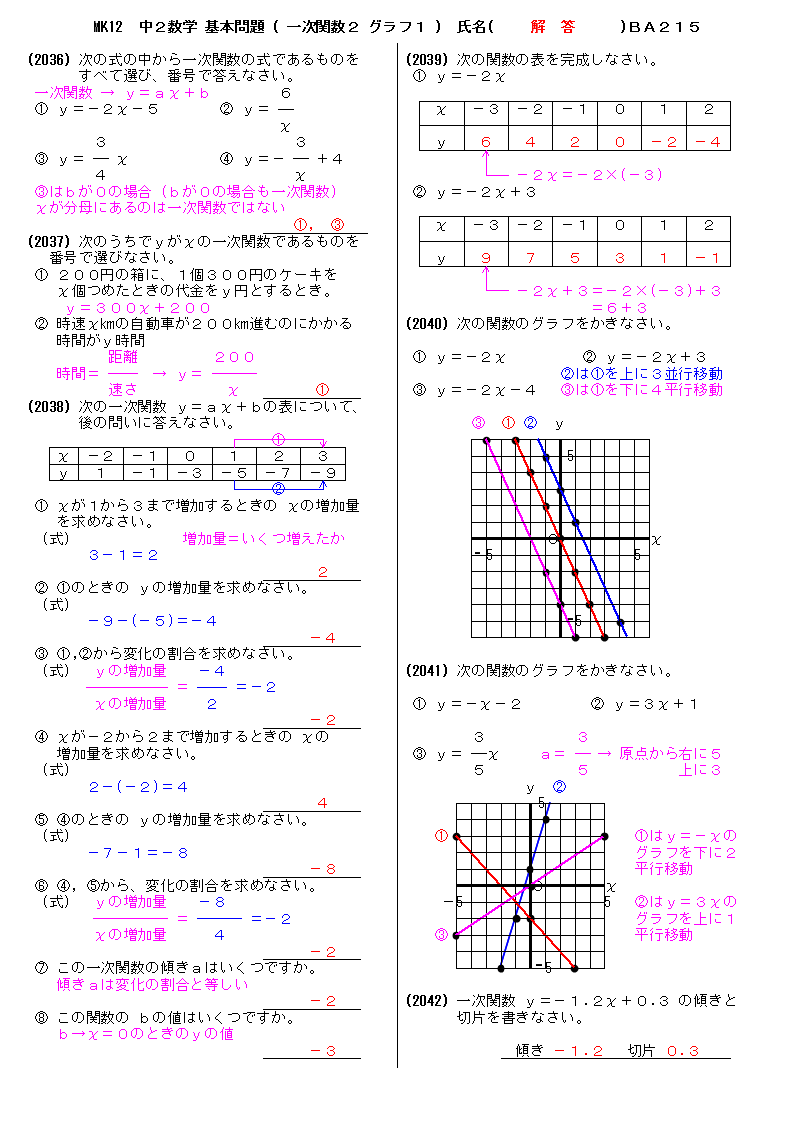



無料 中2数学 基本問題 解答プリント 215 一次関数2 グラフ1
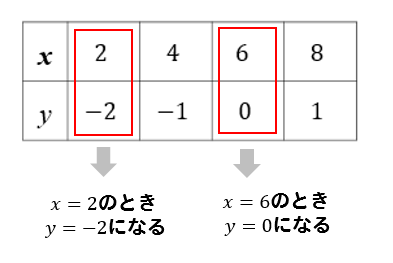
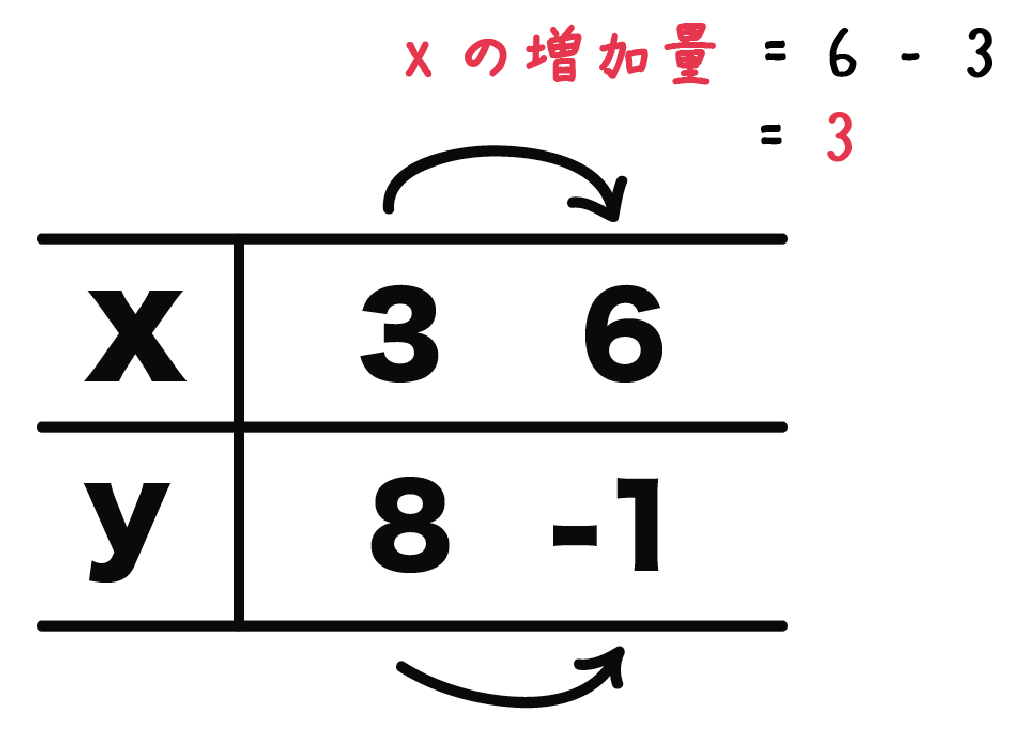
求め方() で求める。 求めることができる(表)3 。 2 1 2元1次方程 ・ 2元1次方程式と1次関数は 2元1次方程式の解と1次関数 式のグラフ() 同じ関係を表していることを理 のグラフ上の点の座標との関係が1 方 解する。 わかる(知)。解説・解法 1次関数の問題で,表が出てくるものがたまに見られます (定期テストにも入試問題にも)。 が,表をよく見てみると,表から「対応するx,yの数値」を2つ読み取ることができますので,結局のところ「 2点を通る1次関数を求める 」問題を解くことになります。 では,求める1次関数を,y=axbとして考えていきましょう。 y=axbとすると,x=2のときy=9ですの・1次関数であるかどうかの判断を、表や式によって できるようにする。 ・いろいろな関数における変化の割合を求める問題に 取り組む。 3 ・グラフをかくことを通じて、1次関数1次関数のグラフ の3 y ax b a や b の持つ意味を考えさせる。




1次関数の導入特徴 Youtube
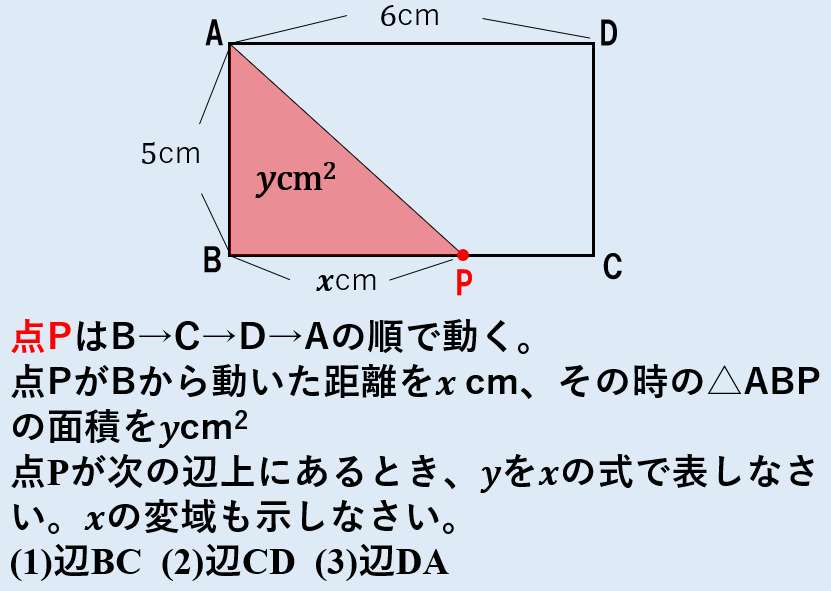



中2数学 一次関数の利用 図形上を点が動く 動点問題 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト
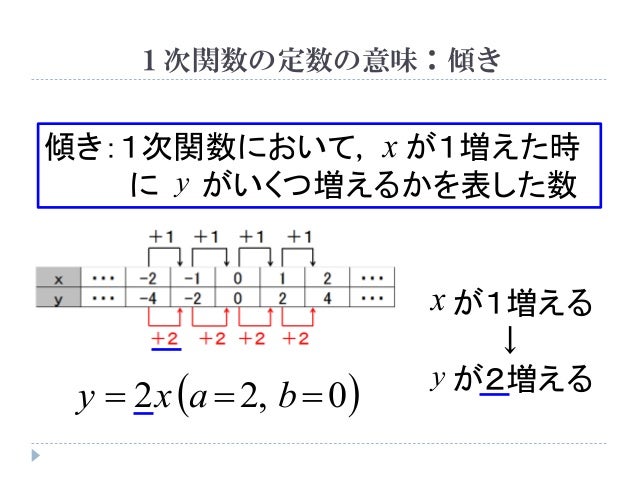
1次関数 y= 3 x+5 では、 「変化の割合」はいつも一定です。 (どの部分で計算しても、 「3」 です。) y=ax+b の "a" の部分にあたるのが、 y=3x+5 であれば「3」ですが、 ここが「変化の割合」を表します。 ですから、 "1次関数の場合は"2次関数と2次関数のグラフ (1) 19 2次関数と2次関数のグラフ (2) 2次関数の最大値・最小値 21 2次関数のグラフと2次方程式 22 2次関数のグラフ二次関数の y=ax^2bxc というグラフを作成してみたいと思います。 定数の a と b と cを変更することができるように、下図のようなデータリストを作成しました。 定数 a の値を1,2,3,4と変えた場合のグラフを作成します。



一次関数 式の求め方をパターン別に問題解説 数スタ




世界一わかりやすい数学問題集中2 3章 一次関数
数学23章一次関数 「一次関数の表,式,グラフ」<基本問題①> 組 番 氏名 1次の にあてはまる数やことばを答えなさい。 (1)yがχの一次関数であるとき,一般的には,a,bを定数として,y= の形の 式で表される。 (2)変化の割合は, で求める。数式 説明 結果 =besselk(15, 1) 変数を 15 とする 1 次の修正ベッセル関数 kn(x) を求めます。② 1次関数について、表、式、グラフを相互に関連付けて理解すること ③ 2元1次方程式を関数を表す式とみること ④ 1次関数を用いて具体的な事象をとらえ説明すること (2)単元の評価規準 数学への 関心・意欲・態度



Http Www Kumamoto Kmm Ed Jp Sugakubraindumps Pdf 2 3 Answer Pdf



Www Tsumugi Ne Jp Member Data Sm2 3 Sm2 3 2 Pdf




一次関数のグラフがスラスラ書ける 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




増減表を使ってグラフを書く 練習編 高校数学の知識庫




一次関数とグラフ 数学の要点まとめ 練習問題一覧




中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




一次関数のグラフ 無料で使える中学学習プリント
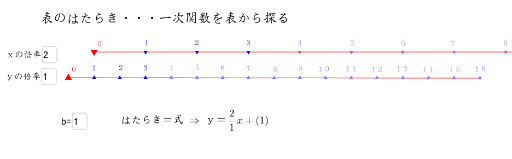



表で一次関数を考える Geogebra



1




Y X Yax Descubre Como Resolverlo En Qanda




中学1年 関数 対応表から式をつくる Youtube
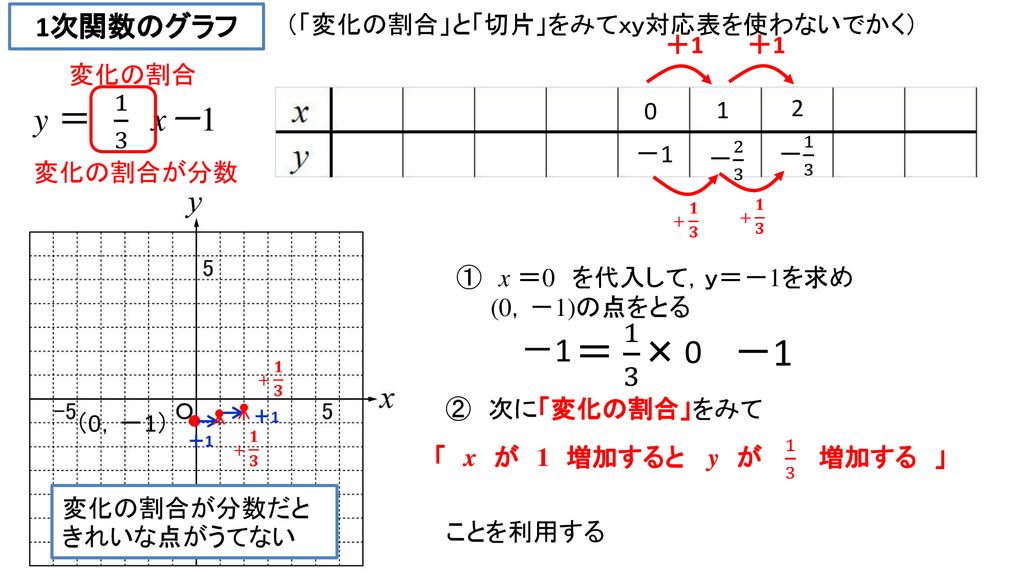



1次関数のグラフ テーマ 目的 xyの対応表を使って 考えられるすべての点をうってグラフをかく以外に 変化の割合を使ってグラフをかく Ppt Download



一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座




中2数学 1次関数の利用 19年2学期期末テスト用 赤城 ᐡᐤᐡ




数学 内容解説資料v2



1
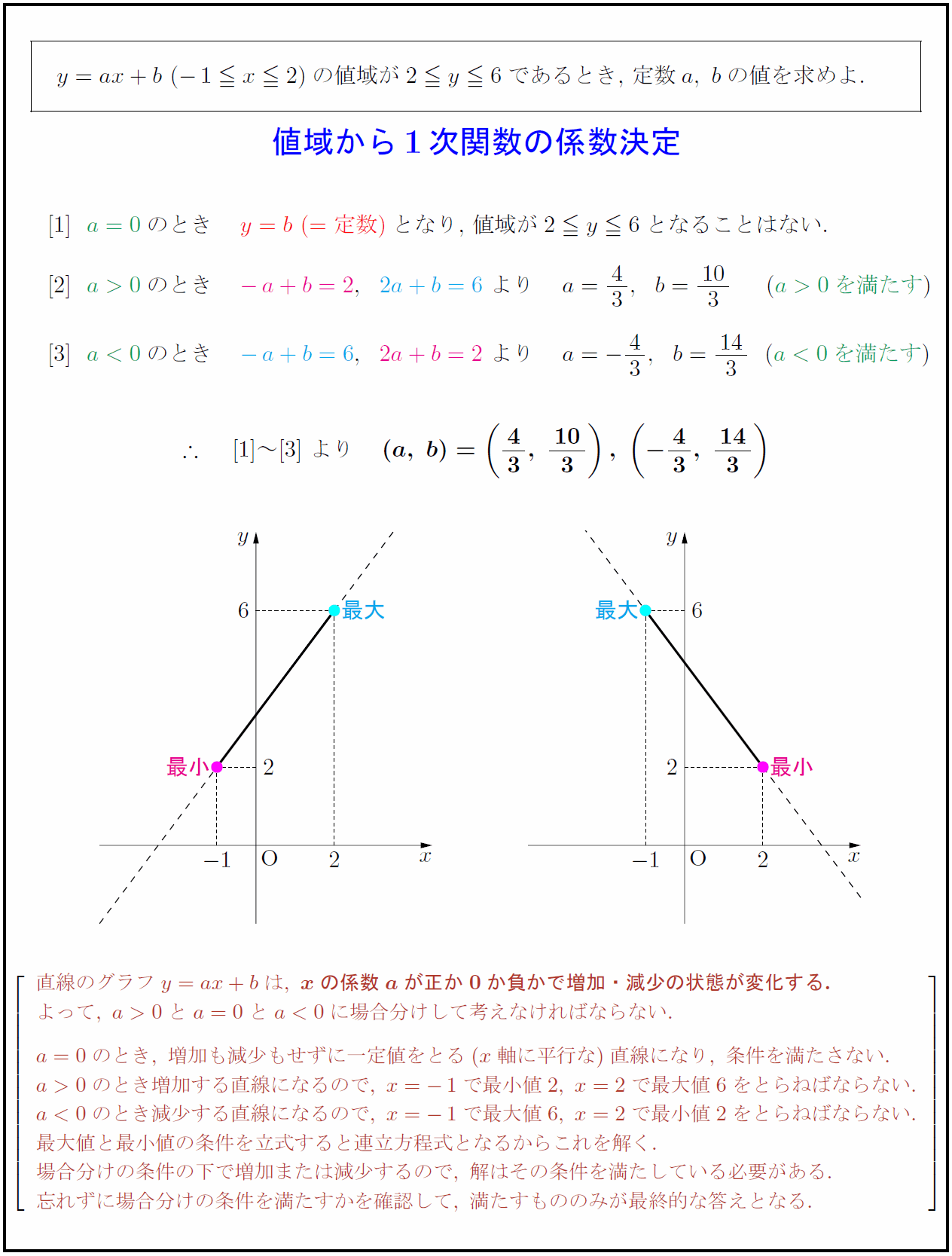



高校数学 値域から1次関数の係数決定 受験の月



1




1 次 関数 の 利用 シモネタ



一次関数 二次関数のグラフや円のグラフを作成したい エクセル13基本講座




1次関数の表から変化の割合 Geogebra




世界一わかりやすい数学問題集中2 3章 一次関数



第2学年 一次関数 単元を貫く導入課題 授業実践記録 アーカイブ一覧 授業支援 サポート資料 数学 中学校 知が啓く 教科書の啓林館




数学 中2 28 一次関数に慣れよう Youtube
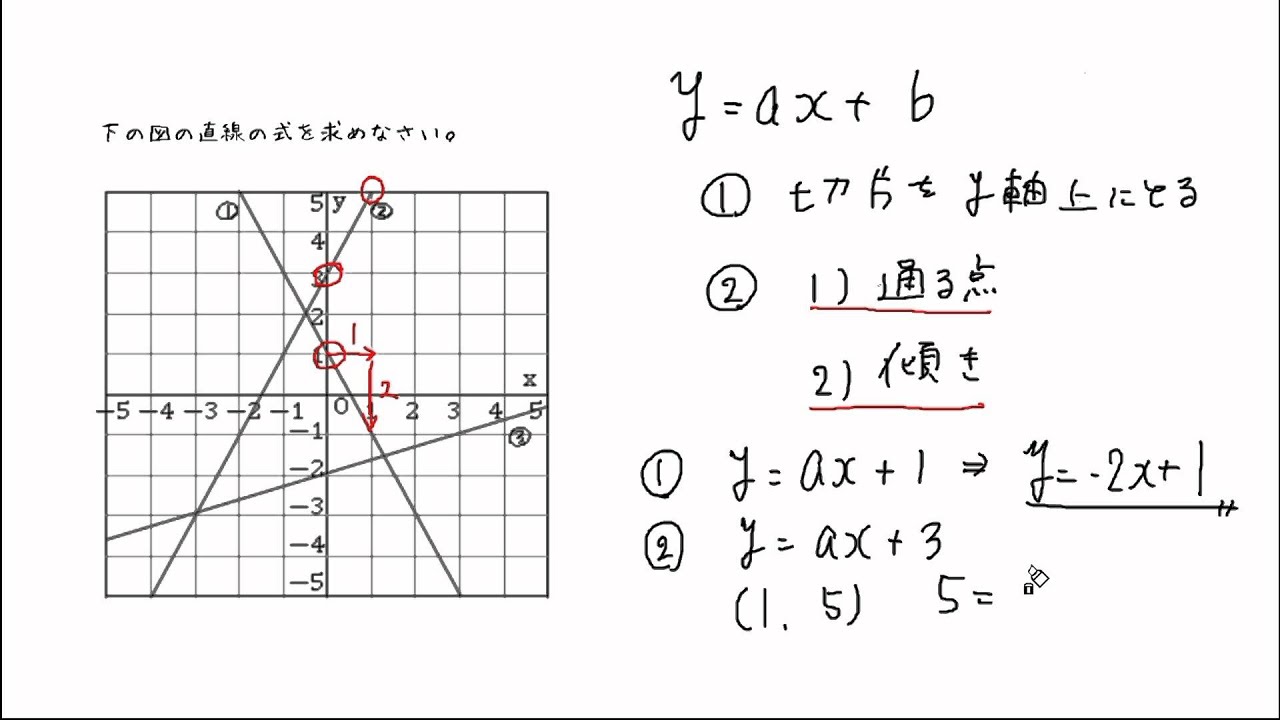



グラフから一次関数の式をもとめる Youtube




数学 一次関数 中学生 数学のノート Clear



一次関数 知らないとできない変化の割合 苦手な数学を簡単に



1次関数のグラフ テーマ 目的 xyの対応表を使って 考えられるすべての点をうってグラフをかく以外に 変化の割合を使ってグラフをかく Ppt Download



中2 1次関数4



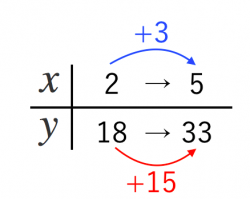
一次関数 X Yの増加量が3秒でわかる2つの求め方 Qikeru 学びを楽しくわかりやすく




一次関数の式を決定1 無料で使える中学学習プリント




中2数学 1次関数のグラフの書き方 例題編 映像授業のtry It トライイット




中2数学 一次関数 一次関数 を大嫌いな人が最初に読む記事 たけのこ塾 勉強が苦手な中学生のやる気をのばす




一次関数とは Yがxの1次式で表される関数 教遊者




1次関数 清水塾



一次関数について基本から分かりやすく解説 具体例で学ぶ数学



ねらい 一次関数のグラフの性質を理解する Ppt Download




4 Yr 1 X Y Descubre Como Resolverlo En Qanda




一次関数の利用 Ict教材eboard イーボード




中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学



Http Www Math Chs Nihon U Ac Jp Ichihara Education Classes 05f Fundmath M No10 Pdf



一次関数の利用を解説 グラフの書き方や解き方を知り入試に活かそう Studyplus スタディプラス




中学2年生 数学 1次関数の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




1次関数のグラフ 数学i フリー教材開発コミュニティ Ftext
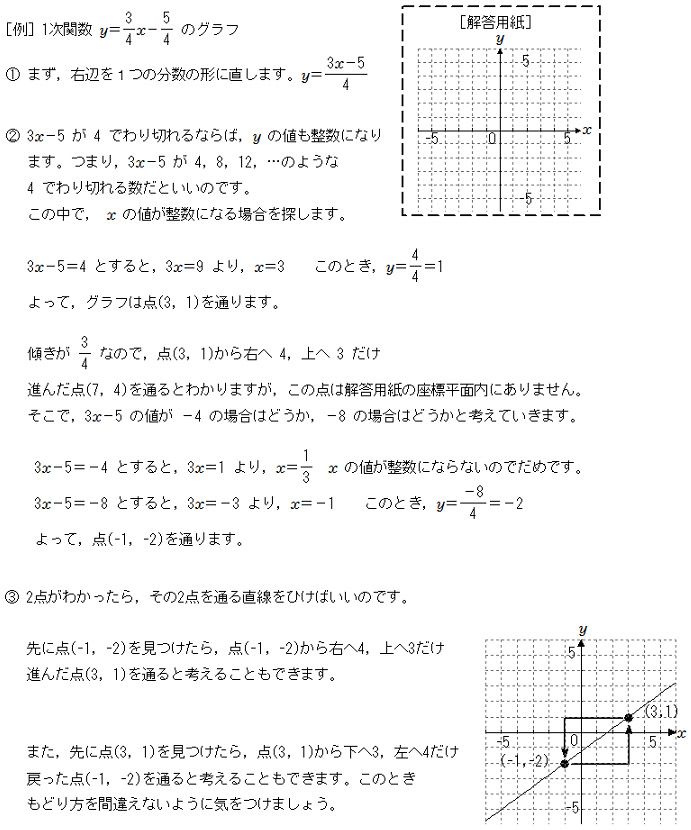



傾きや切片が分数であるグラフのかき方 中学英語 定期テスト対策 ベネッセ教育情報サイト




中学2年生 数学 1次関数 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



1




鉄道の列車運行ダイヤグラム 一次関数のグラフ 全国学力調査2018中学 数学bの解説 テンメイのrun bike




完全版 一次関数のグラフから利用問題まで解き方まとめ 中学数学 理科の学習まとめサイト



中学の一次関数 2次関数の勉強のコツを知って得意になろう




高校数学 1次分数関数の決定 受験の月




1次関数を考える2 2点を通る直線の 方程 式 身勝手な主張
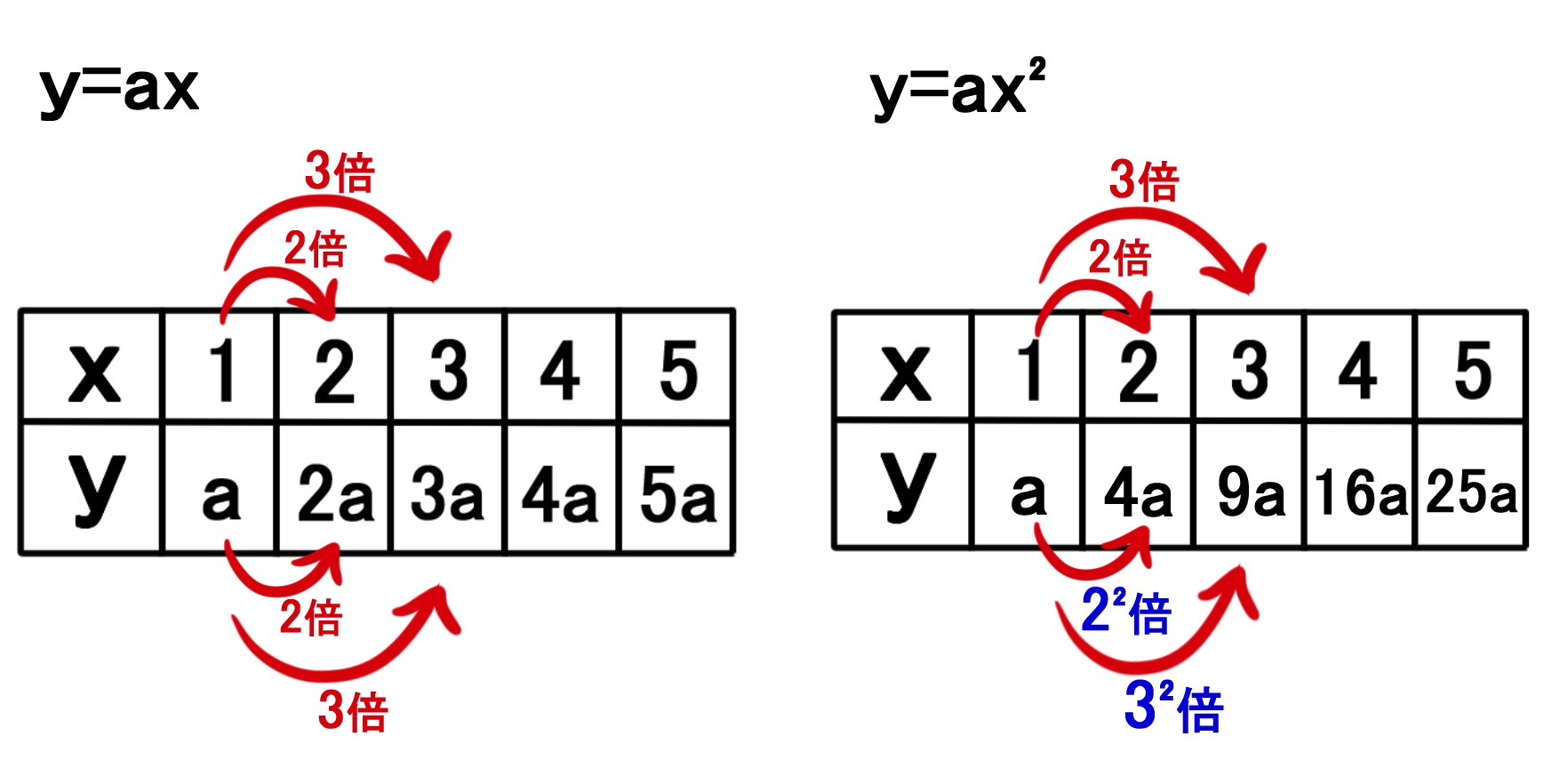



2次関数y Ax のグラフとは バカでもわかる 中学数学




1次関数がさっぱりという方へ 変化の割合と切片について基礎から確認 あんず学習塾のメモ 図表置き場




一次関数の解き方 傾き 切片でのグラフの書き方 交点の求め方 リョースケ大学




Excel エクセルで一次関数を計算し グラフを作る方法 一次関数の解を求める方法



一次関数とは Yがxの1次式で表される関数 教遊者



1次関数のグラフ1




中学校数学 2年生 数量 一次関数 Wikibooks




世界一わかりやすい数学問題集中2 3章 一次関数




二次関数 Wikipedia




切片とは 超簡単 切片を一瞬で求める方法 傾きとの違い 高校生向け受験応援メディア 受験のミカタ



Excel エクセルにて1次関数 一次方程式 の計算 解や傾き とグラフ化の方法 複数も More E Life



中2数学 一次関数の切片を求める2つの方法 Qikeru 学びを楽しくわかりやすく



Www Juen Ac Jp G Katei Nunokawa Function 2 2 4 Pdf



Http Www Juen Ac Jp G Katei Nunokawa Function 2 2 5 Pdf



一次関数 一瞬で答えられる変化の割合 苦手な数学を簡単に




新数学シリーズ




授業実践記録 数学 自ら考え 共に高め合う生徒を育成する指導はどうあればよいか 啓林館
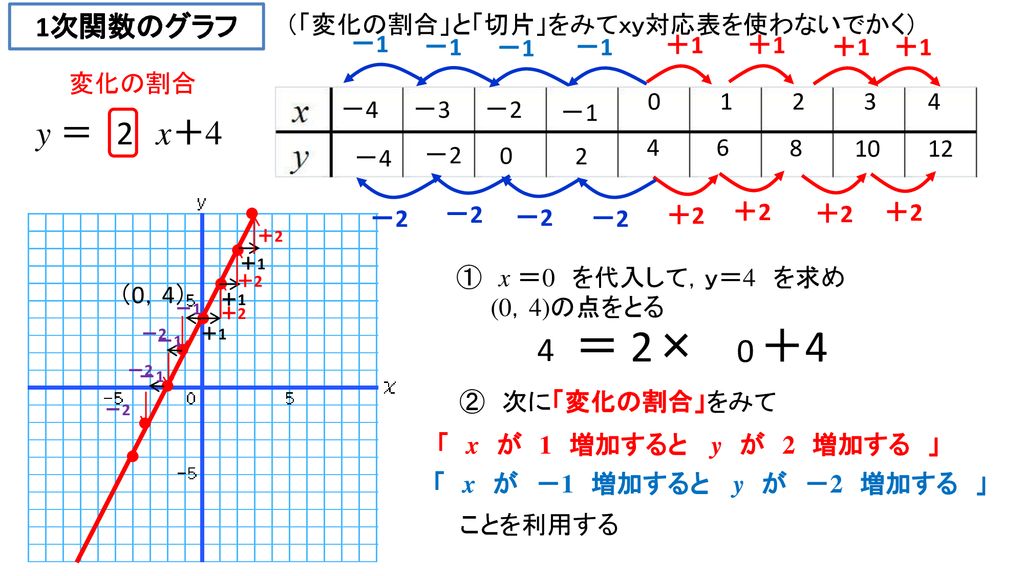



1次関数のグラフ テーマ 目的 xyの対応表を使って 考えられるすべての点をうってグラフをかく以外に 変化の割合を使ってグラフをかく Ppt Download
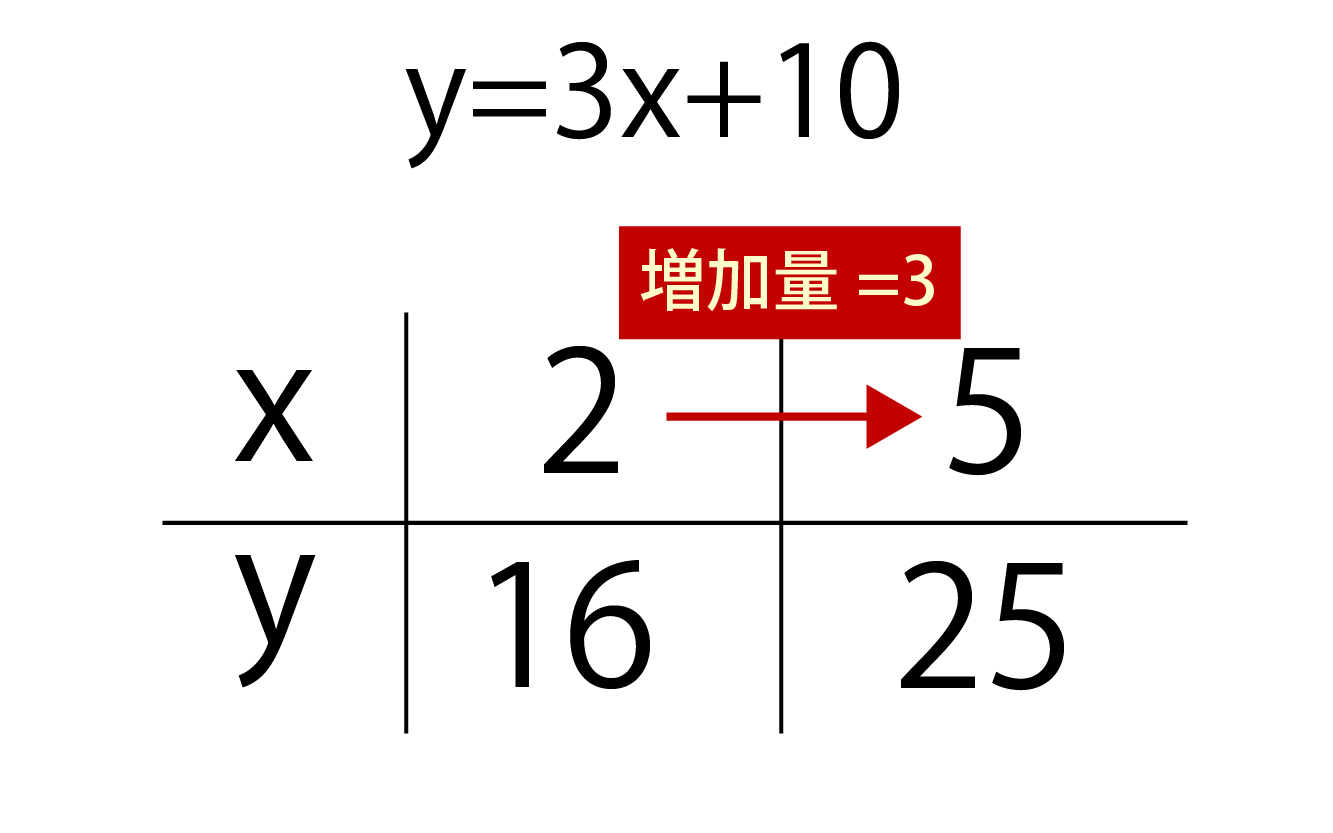



変化の割合 傾きの求め方 二次関数のポイントを即理解しよう 高校生向け受験応援メディア 受験のミカタ



1次関数 グラフから直線の式を求める 勉強ナビゲーター




一次関数 表から式を求めるやり方についてイチから解説 Youtube




1次関数の表から変化の割合 Geogebra



中学2年生 数学 1次関数の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Http Www Pref Oita Jp Uploaded Attachment Pdf




中2数学 きょうの1題 1次関数 7 2 中学数学高校数学個別指導in山形市 数専ゼミ




数学 中2 32 一次関数の式をもとめる 基本編 Youtube




一次関数とは 式とグラフの解説 数学fun



課題学習の指導 数学



一次関数とは グラフの書き方や一次関数の利用問題の解き方 受験辞典
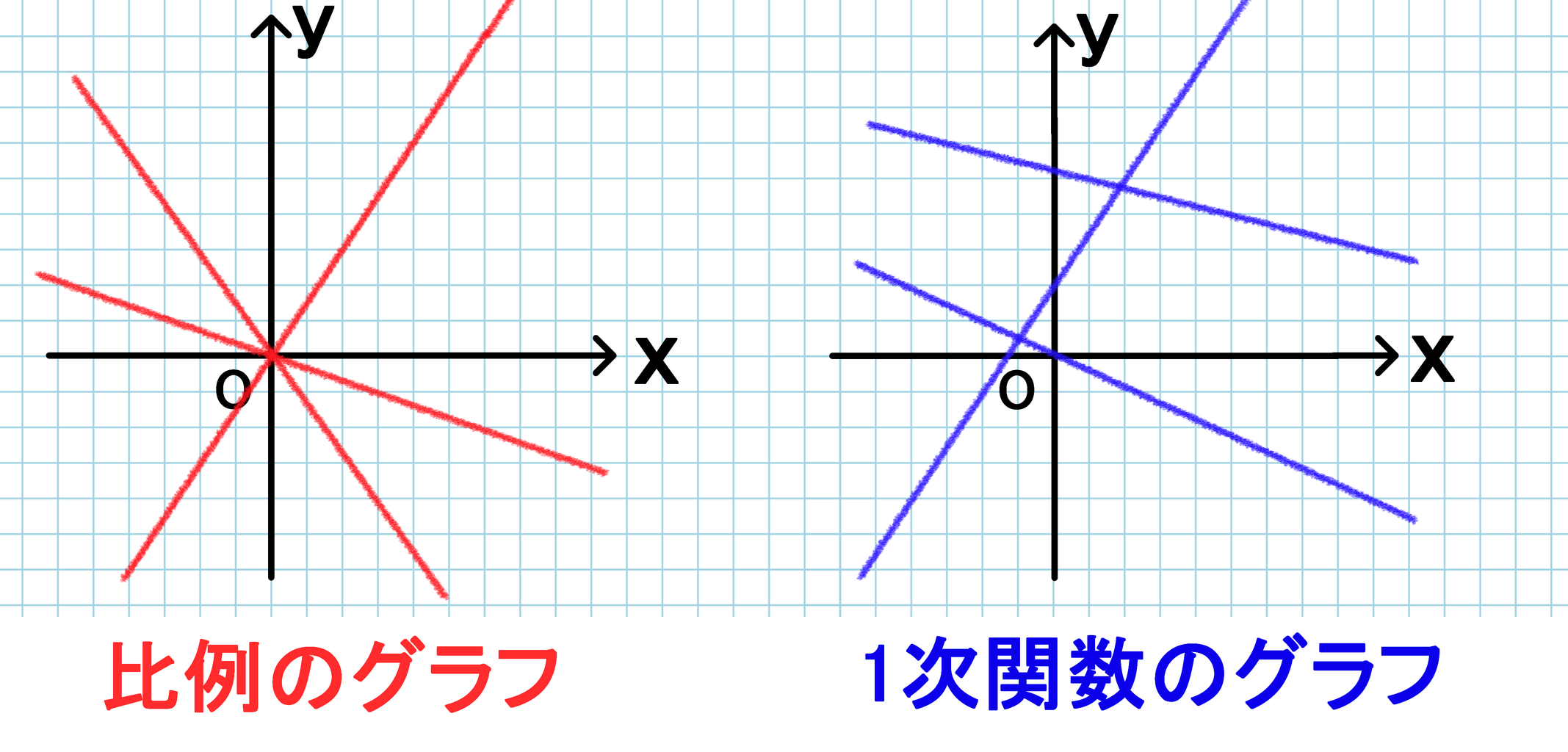



1次関数と比例の違いとは バカでもわかる 中学数学




一次関数




一次関数の表 式 グラフ 中学生 数学のノート Clear



Www Pref Osaka Lg Jp Attach 6629 Jmw 2c3 1 Pdf
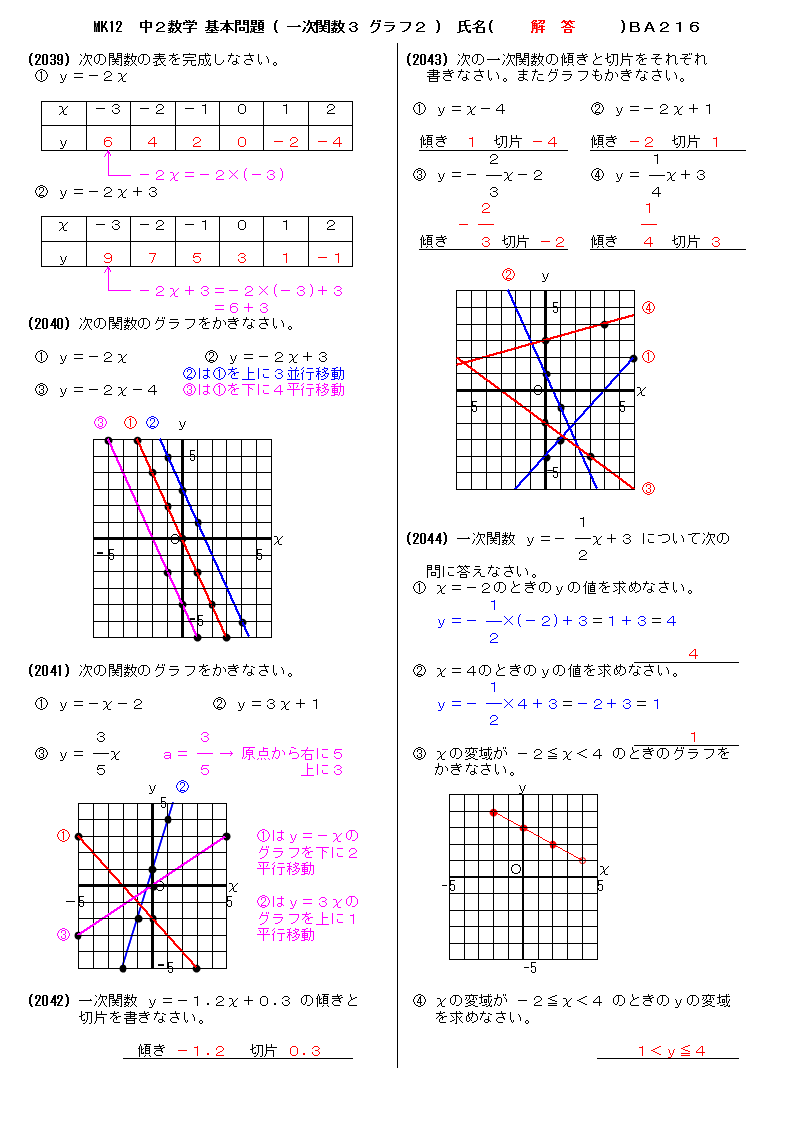



無料 中2数学 基本問題 解答プリント 216 一次関数3 グラフ2




1次関数 1次関数の基礎とグラフ



Http Www7a Biglobe Ne Jp Watmas Dosukyo Circle Reports Linearfunction Pdf



0 件のコメント:
コメントを投稿